
題目列表(包括答案和解析)
已知拋物線C: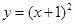 與圓
與圓 有一個公共點A,且在A處兩曲線的切線與同一直線l
有一個公共點A,且在A處兩曲線的切線與同一直線l
(I) 求r;
(II) 設m、n是異于l且與C及M都相切的兩條直線,m、n的交點為D,求D到l的距離。
【解析】本試題考查了拋物線與圓的方程,以及兩個曲線的公共點處的切線的運用,并在此基礎上求解點到直線的距離。
【點評】該試題出題的角度不同于平常,因為涉及的是兩個二次曲線的交點問題,并且要研究兩曲線在公共點出的切線,把解析幾何和導數的工具性結合起來,是該試題的創新處。另外對于在第二問中更是難度加大了,出現了另外的兩條公共的切線,這樣的問題對于我們以后的學習也是一個需要練習的方向。

△ABC中,內角A、B、C成等差數列,其對邊a、b、c滿足 ,求A。
,求A。
【解析】本試題主要考查了解三角形的運用,
因為

【點評】該試題從整體來看保持了往年的解題風格,依然是通過邊角的轉換,結合了三角形的內角和定理的知識,以及正弦定理和余弦定理,求解三角形中的角的問題。試題整體上比較穩定,思路也比較容易想,先將利用等差數列得到角B,然后利用余弦定理求解運算得到A。
若 則給出的數列{
則給出的數列{ 第34項為( )
第34項為( )
A. 1/103 B.1/100 C.103 D.100
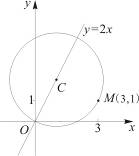
求圓心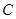 在直線
在直線 上,且經過原點及點
上,且經過原點及點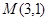 的圓
的圓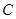 的標準方程.
的標準方程.
【解析】本試題主要考查的圓的方程的求解,利用圓心和半徑表示圓,首先設圓心C的坐標為( ),然后利用
),然后利用 ,得到
,得到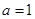 ,從而圓心
,從而圓心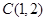 ,半徑
,半徑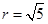 .可得原點 標準方程。
.可得原點 標準方程。
解:設圓心C的坐標為( ),...........2分
),...........2分
則 ,即
,即
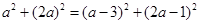 ,解得
,解得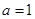 ........4分
........4分
所以圓心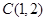 ,半徑
,半徑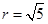 ...........8分
...........8分
故圓C的標準方程為: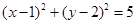 .......10分
.......10分
已知函數
(I) 討論f(x)的單調性;
(II) 設f(x)有兩個極值點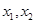 若過兩點
若過兩點 的直線I與x軸的交點在曲線
的直線I與x軸的交點在曲線 上,求α的值。
上,求α的值。
【解析】本試題考查了導數在研究函數中的運用。第一就是三次函數,通過求解導數,求解單調區間。另外就是運用極值的概念,求解參數值的運用。
【點評】試題分為兩問,題面比較簡單,給出的函數比較常規,,這一點對于同學們來說沒有難度但是解決的關鍵還是要看導數的符號的實質不變,求解單調區間。第二問中,運用極值的問題,和直線方程的知識求解交點,得到參數的值。
(1)

1. 構造向量 ,
, ,所以
,所以 ,
, .由數量積的性質
.由數量積的性質 ,得
,得 ,即
,即 的最大值為2.
的最大值為2.
2. ∵ ,令
,令 得
得 ,所以
,所以 ,當
,當 時,
時, ,當
,當 時,
時, ,所以當
,所以當 時,
時, .
.
3.∵ ,∴
,∴ ,
, ,又
,又 ,∴
,∴ ,則
,則 ,所以周期
,所以周期 .作出
.作出 在
在 上的圖象知:若
上的圖象知:若 ,滿足條件的
,滿足條件的 (
( )存在,且
)存在,且 ,
, 關于直線
關于直線 對稱,
對稱, ,
, 關于直線
關于直線 對稱,∴
對稱,∴ ;若
;若 ,滿足條件的
,滿足條件的 (
( )存在,且
)存在,且 ,
, 關于直線
關于直線 對稱,
對稱, ,
, 關于直線
關于直線 對稱,
對稱,
 ∴
∴ .
.
4. 不等式 (
( )表示的區域是如圖所示的菱形的內部,
)表示的區域是如圖所示的菱形的內部,
∵
 ,
,
當 ,點
,點 到點
到點 的距離最大,此時
的距離最大,此時 的最大值為
的最大值為 ;
;
當 ,點
,點 到點
到點 的距離最大,此時
的距離最大,此時 的最大值為3.
的最大值為3.
5. 由于已有兩人分別抽到5和14兩張卡片,則另外兩人只需從剩下的18張卡片中抽取,共有 種情況.抽到5 和14的兩人在同一組,有兩種情況:
種情況.抽到5 和14的兩人在同一組,有兩種情況:
(1) 5 和14 為較小兩數,則另兩人需從15~20這6張中各抽1張,有 種情況;
種情況;
(2) 5 和14 為較大兩數,則另兩人需從1~4這4張中各抽1張,有 種情況.
種情況.
于是,抽到5 和14 兩張卡片的兩人在同一組的概率為 .
.
 6. ∵
6. ∵ ,∴
,∴ ,
,
設 ,
, ,則
,則 .
.
作出該不等式組表示的平面區域(圖中的陰影部分 ).
).
令 ,則
,則 ,它表示斜率為
,它表示斜率為 的一組平行直線,易知,當它經過點
的一組平行直線,易知,當它經過點 時,
時, 取得最小值.
取得最小值.
解方程組 ,得
,得 ,∴
,∴
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com