日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

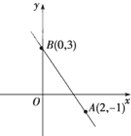（第三、四層次學(xué)校的學(xué)生做次題）
已知二次函數(shù)h（x）=ax²+bx+c（c＞0），其導(dǎo)函數(shù)y=h′（x）的圖象如下，且f（x）=lnx-h（x）．
（1）求a，b的值；
（2）若函數(shù)f（x）在(

1

2

，m+

1

4

)上是單調(diào)遞減函數(shù)，求實(shí)數(shù)m的取值范圍；
（3）若函數(shù)y=2x-lnx（x∈[1，4]）的圖象總在函數(shù)y=f（x）的圖象的上方，求c的取值范圍．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

一、ADBCC  CCBBA  DC

二、13. ,;14. ；15. ．16.

三、

17.

解: (Ⅰ)由, 是三角形內(nèi)角，得……………..

∴ ………………………………………..

  …………………………………………………………6分

(Ⅱ) 在中,由正弦定理， ，

…, ,

由余弦定理得:

                =………………………………12分

18.

解：（I）已知，

       只須后四位數(shù)字中出現(xiàn)2個(gè)0和2個(gè)1.

                                             …………4分

   （II）的取值可以是1，2，3，4，5，.

                                                              …………8分

       的分布列是

1

2

3

4

5

P

                                                                                                      …………10分

                 …………12分

   （另解：記

       .）

19.

證明： 解法一：（1）取PC中點(diǎn)M，連結(jié)ME、MF，則MF∥CD，MF=CD，又AE∥CD，AE=CD，∴AE∥MF，且AE=MF，∴四邊形AFME是平行四邊形，∴AF∥EM，∵AF平面PCE，∴AF∥平面PCE. …………………………………(4分)

         (2)∵PA⊥平面ABCD，CD⊥AD. ∴CD⊥PD，∴∠PDA是二面角P-CD-B的平面角，即∠PDA=45°，   ………………………………………………………………(6分)

∴△PAD是等腰直角三角形，∴AF⊥PD，又AF⊥CD，∴AF⊥平面PCD，而EM∥AF，∴EM⊥平面PCD. 又EM平面PEC，∴面PEC⊥面PCD. 在平面PCD內(nèi)過F作FH⊥PC于H，則FH就是點(diǎn)F到平面PCE的距離. …………………………………(10分)

由已知，PD=，PF=，PC=，△PFH∽△PCD，∴，

∴FH=.           ………………………………………………………………(12分)

       解法二：（1）取PC中點(diǎn)M，連結(jié)EM，

=+=，∴AF∥EM，又EM平面PEC，AF平面PEC，∴AF∥平面PEC. ………………………………………(4分)

（2）以Ａ為坐標(biāo)原點(diǎn)，分別以所在直線為x、y、z

軸建立坐標(biāo)系.　∵PA⊥平面ABCD，CD⊥AD，∴CD⊥PD，

∴∠PDA是二面角P-CD-B的平面角，即∠PDA=45°. ……(6分)

∴A(0, 0, 0), P(0, 0, 2), D(0, 2, 0), F(0, 1, 1), E, C(3, 2, 0)，

設(shè)平面PCE的法向量為=(x, y, z)，則⊥，⊥，而=（-，0，2），

=（，2，0），∴-x+2z=0，且x+2y=0，解得y=-x，z=x. 取x=4

得=(4, -3, 3)，………………………………………………………………(10分)

又=（0，1，-1），

故點(diǎn)F到平面PCE的距離為d=.…………(12分)

20.

 解:1)函數(shù).又,故為第一象限角,且.

   函數(shù)圖像的一條對(duì)稱軸方程式是: 得又c為半點(diǎn)焦距，

   由知橢圓C的方程可化為

                             （1）

   又焦點(diǎn)F的坐標(biāo)為（），AB所在的直線方程為

                               （2）                     （2分)

  （2）代入（1）展開整理得

                      （3）

   設(shè)A（），B（），弦AB的中點(diǎn)N（），則是方程（3）的兩個(gè)不等的實(shí)數(shù)根，由韋達(dá)定理得

                       （4）

         即為所求。                    （5分）

2）與是平面內(nèi)的兩個(gè)不共線的向量，由平面向量基本定理，對(duì)于這一平面內(nèi)的向量，有且只有一對(duì)實(shí)數(shù)使得等式成立。設(shè)由1）中各點(diǎn)的坐標(biāo)可得：

又點(diǎn)在橢圓上，代入（1）式得

化為：        （5）

   由（2）和（4）式得

   又兩點(diǎn)在橢圓上，故1有入（5）式化簡得：

由得到又是唯一確定的實(shí)數(shù)，且，故存在角，使成立，則有

若，則存在角使等式成立；若由與于是用代換，同樣證得存在角使等式：成立.

綜合上述，對(duì)于任意一點(diǎn)，總存在角使等式：成立.

                                                                     （12分）

21．解：(Ⅰ)  

所以函數(shù)在上是單調(diào)減函數(shù). …………………………4分

 (Ⅱ) 證明:據(jù)題意且x₁<x₂<x₃,

由(Ⅰ)知f (x₁)>f (x₂)>f (x₃),  x₂=…………………………6分

…………………8分

即ㄓ是鈍角三角形……………………………………..9分

(Ⅲ) 假設(shè)ㄓ為等腰三角形，則只能是

即

  ①          …………………………………………

而事實(shí)上,    ②

由于,故(2)式等號(hào)不成立.這與式矛盾. 所以ㄓ不可能為等腰三角形..13分

22．

解：⑴∵，又，為遞增數(shù)列即為，

當(dāng)時(shí)，恒成立，當(dāng)時(shí)，的最大值為。∴ 。∴b的取值范圍是：                   （6分）

⑵     ①又       ②

①-②：

，

當(dāng)時(shí)，有成立，

得與同號(hào)，于是由遞推關(guān)系得與同號(hào)，因此只要就可推導(dǎo)。又

，又    ，

即首項(xiàng)的取值范圍是

                                                                      （13分）