
重慶八中高2009級高三下第一次月考
數學試題(文科)
一、選擇題:本大題共12小題,每題5分,共60分.在每小題給出的四個選項中,只有一項是符合題目要求的.
1.集合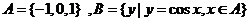 ,則
,則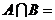 ( )
( )
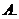
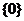

2.若點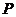 是平面
是平面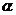 外一點,則下列命題中正確的是( )
外一點,則下列命題中正確的是( )
A.過點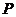 只能作一條直線與平面
只能作一條直線與平面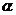 相交 B.過點
相交 B.過點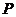 可作無數條直線與平面
可作無數條直線與平面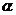 垂直
垂直
C.過點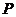 只能作一條直線與平面
只能作一條直線與平面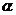 平行 D.過點
平行 D.過點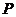 可作無數條直線與平面
可作無數條直線與平面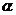 平行
平行
3.經過圓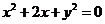 的圓心
的圓心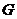 ,且與直線
,且與直線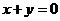 垂直的直線方程是( )
垂直的直線方程是( )
A.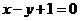 B.
B.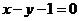 C.
C.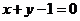 D.
D.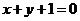
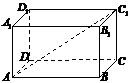 4.如圖,在長方體ABCD-A1B
4.如圖,在長方體ABCD-A1B
A.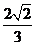 B.
B.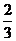 C.
C. D.
D.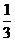
5.右圖為函數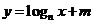 的圖象,其中
的圖象,其中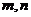 為常數,則下列結論正確的是
( )
為常數,則下列結論正確的是
( )
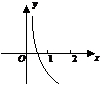 |
A. 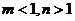 B.
B.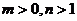
C. 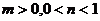 D.
D.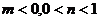
6.若函數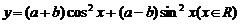 的值恒等于
的值恒等于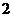 ,則點
,則點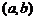 關于原點對稱的點的坐標是( )
關于原點對稱的點的坐標是( )
A.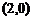 ;
B.
;
B.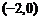 ;
C.
;
C.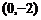 ; D.
; D.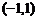
7.正數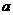 、
、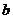 的一個等差中項為
的一個等差中項為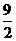 ,一個等比中項為
,一個等比中項為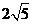
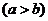 ,則
,則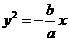 的焦點坐標為(
)
的焦點坐標為(
)
A. 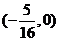 B.
B.
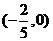 C.
C.
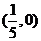 D.
D.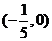
8.已知函數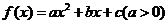 ,
,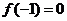 ,則
,則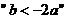 是
是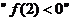 的(
)
的(
)
A.充要條件 B.充分不必要條件
C.必要不充分條件 D.既不充分也不必要條件
9.若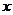 、
、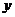 滿足不等式組
滿足不等式組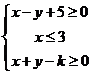 ,且
,且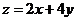 的最小值為
的最小值為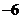 ,則
,則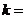 ( )
( )
A.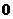 B.
B. 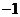 C.
C.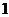 D.
D.
10.已知數列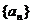 、
、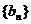 都是公差為1的等差數列,其首項分別為
都是公差為1的等差數列,其首項分別為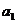 、
、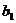 ,且
,且 ,
,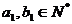 .設
.設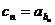 (
(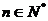 ),則數列
),則數列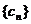 的前10項和等于( )
的前10項和等于( )
A.55 B.
11.平面直角坐標系中,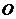 為坐標原點,已知點
為坐標原點,已知點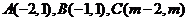 ,若點
,若點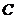 滿足
滿足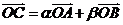 ,且
,且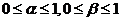 ,則
,則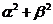 的最大值為( )
的最大值為( )
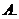
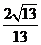
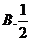
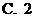
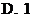
12.雙曲線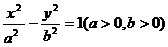 的右支上存在一點,它到右焦點及左準線的距離相等,則雙曲線離心率的取值范圍是( )
的右支上存在一點,它到右焦點及左準線的距離相等,則雙曲線離心率的取值范圍是( )
A.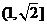 B.
B.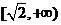 C.
C.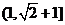 D.
D.
二、填空題:本大題共4小題,每題4分,共16分.
13.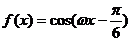 最小正周期為
最小正周期為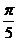 ,其中
,其中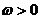 ,則
,則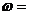 _______________
_______________
14.已知各頂點都在一個球面上的正四棱柱底面邊長為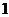 ,體積為
,體積為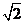 ,則這個球的表面積是________________
,則這個球的表面積是________________
15.若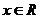 且滿足條件
且滿足條件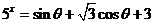 ,則二次函數
,則二次函數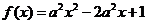 (
(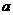 為非
為非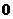 常數)的值域為_________________
常數)的值域為_________________
16.已知三棱錐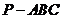 的三條側棱
的三條側棱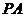 、
、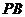 、
、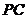 的長分別為
的長分別為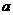 、
、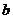 、
、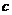 ,且兩兩垂直,并滿足
,且兩兩垂直,并滿足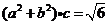 ,當三棱錐體積最大時,側面
,當三棱錐體積最大時,側面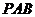 與底面
與底面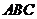 成
成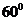 ,則三棱錐體積最大時
,則三棱錐體積最大時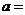 __________________
__________________
三、解答題:本題共6小題,共74分,解答應寫出文字說明、證明過程或演算步驟.
 17.如圖,在四棱錐
17.如圖,在四棱錐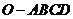 中,底面
中,底面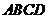 是邊長為2的菱形,
是邊長為2的菱形, 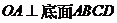 ,
, 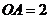 ,
,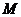 為
為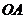 的中點,
的中點,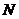 為
為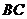 的中點,
的中點,
(1)證明:直線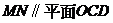 ;
;
(2)求異面直線AB與MD所成角的余弦值;
(3)求點B到平面OCD的距離。
18.在 中,
中,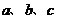 分別是角
分別是角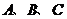 的對邊,且
的對邊,且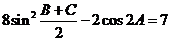
(1)求角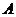 的大小
的大小
(2)若 ,
,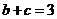 ,求
,求 的面積
的面積
19.三棱錐被平行于底面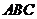 的平面所截得的幾何體如圖所示,截面為
的平面所截得的幾何體如圖所示,截面為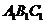 ,
,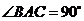 ,
,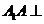 平面
平面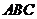 ,
,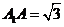 ,
,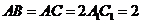 ,
,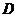 為
為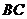 中點.
中點.
 (Ⅰ)證明:平面
(Ⅰ)證明:平面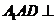 平面
平面 ;
;
(Ⅱ)求二面角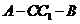 的大小.
的大小.
20.已知函數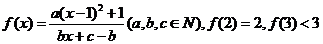 ,且
,且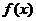 的圖像按向量
的圖像按向量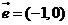 平移后得到的圖像關于原點對稱.
平移后得到的圖像關于原點對稱.
(1)求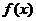 的解析式;
的解析式;
(2)設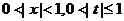 .求證:
.求證: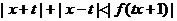 .
.
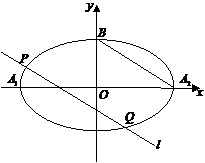 21.已知A1、A2、B是橢圓
21.已知A1、A2、B是橢圓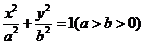 的頂點(如圖),直線
的頂點(如圖),直線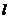 與橢圓交于異于橢圓頂點的P、Q兩點,且
與橢圓交于異于橢圓頂點的P、Q兩點,且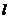 //A2B。若此橢圓的離心率為
//A2B。若此橢圓的離心率為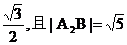
(I)求此橢圓的方程;
(II)設直線A1P和直線BQ的傾斜角分別為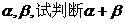 是否為定值?若是,求出此定值;若不是,請說明理由。
是否為定值?若是,求出此定值;若不是,請說明理由。
22.由函數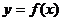 確定數列
確定數列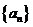 ,
, ,若函數
,若函數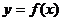 的反函數
的反函數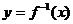 確定數列
確定數列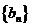 ,且
,且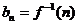 ,則稱數列
,則稱數列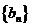 是數列
是數列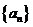 的“反數列”
的“反數列”
⑴若函數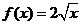 確定數列
確定數列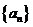 的反數列為
的反數列為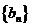 ,求
,求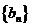 的通項公式;
的通項公式;
⑵對⑴式中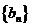 ,不等式
,不等式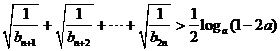 對任意的正整數
對任意的正整數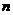 恒成立,求實數
恒成立,求實數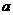 的取值范圍;
的取值范圍;
⑶設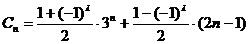
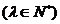 ,若數列
,若數列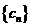 的反數列為
的反數列為
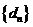 ,設
,設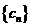 與
與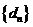 的公共項組成的數列為
的公共項組成的數列為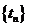 ,求數列
,求數列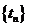 的前
的前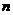 項和
項和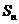 .
.
一選擇題
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
A
D
D
B
D
B
A
C
D
C
 提示:10.解:數列
提示:10.解:數列 、
、 都是公差為1的等差數列,其首項分別為
都是公差為1的等差數列,其首項分別為 、
、 ,且
,且 ,
, .設(
.設( ),則
),則

 ,所以
,所以 是等差數列,所以
是等差數列,所以 的前
的前 項和
項和
11.由題 ,消去
,消去 可得:
可得: ,又由題有:
,又由題有: ,由以上條件可得:點
,由以上條件可得:點 的軌跡為如圖所示的線段
的軌跡為如圖所示的線段 ,而
,而 表示點
表示點 到坐標原點的距離的平方,所以
到坐標原點的距離的平方,所以
12.設點 到左準線的距離為
到左準線的距離為 ,則由雙曲線的第二定義有:
,則由雙曲線的第二定義有: ,由題有
,由題有 ,所以
,所以 ,又由第一定義
,又由第一定義 (
( 在右支上),所以
在右支上),所以 ,
, ,又由點
,又由點 在右支上,則
在右支上,則 ,
, ,解得:
,解得: ,而
,而 ,所以
,所以
二.填空題
13.  14.
14.  15.
15. 16. 1
16. 1
提示:15.

 ,
, ,
, 
 在
在 單調遞減,
單調遞減,
 16.如圖,設三棱錐得體積為
16.如圖,設三棱錐得體積為 ,
, ,當且僅當
,當且僅當 時三棱錐體積最大,過點
時三棱錐體積最大,過點 作
作 ,連接
,連接 ,由題可知
,由題可知 平面
平面 ,由三垂線定理可知
,由三垂線定理可知 為側面
為側面 與底面
與底面 成的角,所以
成的角,所以 ,而用等面積法可知:
,而用等面積法可知: ,
, ,所以
,所以 ,代入
,代入 ,得
,得
三.解答題
17.解:(1)取OB中點E,連接ME,NE
 …………………………………………2分
…………………………………………2分
又 …………………………………4分
…………………………………4分
 …………………………………………………………5分
…………………………………………………………5分
(2)連接

 為異面直線
為異面直線 與
與 所成的角(或其補角)…7分
所成的角(或其補角)…7分
由于 ,所以
,所以 ,
, ,
, 為等腰三角形,
為等腰三角形, ……………………………………………………9分
……………………………………………………9分
(3)解法一:連接 ,設點B到平面OCD的距離為
,設點B到平面OCD的距離為 ,
,
由 ,
, ,
, ,
, 為等腰三角形,
為等腰三角形,
 的高為
的高為 ,
, ………11分
………11分
又 ,又
,又

點B到平面OCD的距離為 …………………………………………13分
…………………………………………13分
解法二: 點A和點B到平面OCD的距離相等,取
點A和點B到平面OCD的距離相等,取 的中點P連
的中點P連
接OP,過點作 于點Q,
于點Q, ,又
,又

 又
又  ,
,
線段AQ的長就是點A到平面OCD的距離, ………………………………12分
由題可知: ,
, ,在
,在 中
中 .……13分
.……13分
18.解: 在
在 中,
中,
 ………………………………3分
………………………………3分
 ……5分
……5分
 ……………7分
……………7分
(2)由余弦定理得 ,又由已知和(1)可知:
,又由已知和(1)可知:

 …………………………10分
…………………………10分


 ………………………………13分
………………………………13分
 19.解:(Ⅰ)
19.解:(Ⅰ)
 平面
平面 平面
平面 ,
,
 …………2分
…………2分
在 中,
中, ,
, 為
為 中點
中點
 .……………4分
.……………4分
 平面
平面 ,
, 平面
平面
 平面
平面 .……………6分
.……………6分
(Ⅱ)如圖,作 交
交 于
于 點,連接
點,連接 ,
,
由已知得 平面
平面 .
. 是
是 在面
在面 內的射影.
內的射影.
由三垂線定理知 ,
, 為二面角
為二面角 的平面角.……………9分
的平面角.……………9分
過 作
作 交
交 于
于 點,則
點,則 ,
, ,
,
 .在
.在 中,
中, .…………11分
.…………11分
在 中,
中, .
. ,
,
即二面角 為
為 .………………………………13分
.………………………………13分
20.解答:(1) ,
, ,又因為
,又因為 按向量
按向量 平移后得函數
平移后得函數 ……..2分
……..2分
由g(x)圖像關于原點對稱得g(-x)=-g(x),即 ,
,
 ,
, …………………………………………………...4分
…………………………………………………...4分
由
當 (舍)所以
(舍)所以 …….6分
…….6分
(2)證明:因為
所以 ……………………………………8分
……………………………………8分
故 ……………………………………9分
……………………………………9分
又 ……………………12分
……………………12分
所以 .……………………………………13分
.……………………………………13分
21.解:(I)由已知可得
 ……2分 所以
……2分 所以 …3分 橢圓方程為
…3分 橢圓方程為 ……5分
……5分
(II) ,且定值為
,且定值為 由(I),A2(2,0),B(0,1),且
由(I),A2(2,0),B(0,1),且 //A2B
//A2B
所以直線 的斜率
的斜率 ………………………………6分
………………………………6分
設直線 的方程為
的方程為
 解得:
解得:
 即
即
 ………………………………………………8分
………………………………………………8分

 ……………………9分
……………………9分
又因為




 又
又

 是定值。…………12分
是定值。…………12分
22.(1) (
( 為正整數),
為正整數),
所以數列 的反數列為
的反數列為 的通項
的通項 (
( 為正整數). …………3分
為正整數). …………3分
(2)對于(1)中 ,不等式化為
,不等式化為 .
.
設 ,
,
 ,
,
∴數列 單調遞增, 所以,
單調遞增, 所以,  ,要使不等式恒成立,只要
,要使不等式恒成立,只要 .
.
∵ ,∴
,∴ ,又
,又 ,
,
所以,使不等式對于任意正整數 恒成立的
恒成立的 的取值范圍是
的取值范圍是 .…………7分(3)設公共項
.…………7分(3)設公共項 為正整數.
為正整數.
①當 為奇數時,
為奇數時, .
.  ,
,
則 (表示
(表示 是
是 的子數列),
的子數列), .所以
.所以 的前
的前 項和
項和 .
.
② 當 為偶數時,
為偶數時, .
. ,則
,則 ,同樣有
,同樣有 ,
, .所以
.所以 的前
的前 項和
項和 .
…………12分
.
…………12分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com