日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

撫州一中2009屆高三第四次模擬考試

數學試卷（理）

命題人 ：高三數學組                   考試時間 ：2009.5

第Ⅰ卷（選擇題　共60分）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

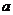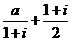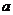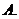
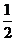
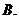
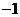
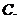
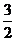
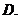
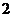
1．設高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。是實數，且高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。是純虛數，則高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的值是　　　　　　　　　　　（　　）

試題詳情

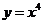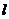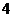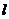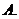
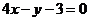
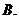
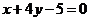
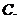
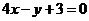
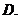
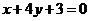
高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。            　    　高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。        　    　　高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。            　    　　高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

2．若曲線高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的一條切線高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的斜率為高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，則切線高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的方程是　　　　　　　　（　　）

試題詳情

高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                             高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。   

試題詳情

高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                                  高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

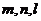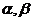3．已知三條不重合的直線高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，兩個不重合的平面高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，有下列命題

試題詳情

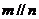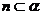
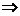
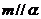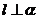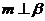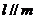
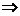
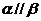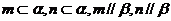
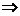
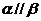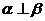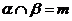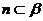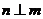
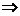
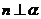①高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。；      ②高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。；

試題詳情

③高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。；

試題詳情

④高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。.

其中正確的命題個數是                                                  （　　）

試題詳情

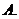
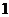
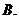
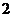
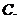
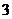
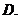
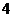
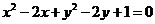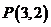高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                         高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                        高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                        高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

4．從圓高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。外一點高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。向這個圓作兩條切線，則兩切線夾角的余弦值為（ ）

試題詳情

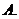
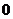
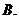
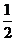
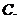
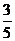
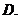
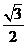
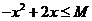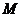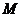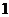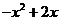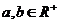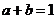高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。      　　　　高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                    高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

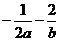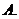
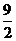
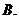
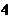
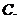
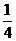
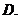
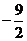
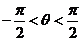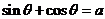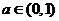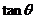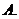
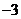
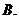
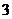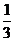
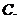
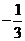5．對于使高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。成立的所有常數高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。中，我們把高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的最小值高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。叫做高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的上確定界.若高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，且高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，則高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的上確界為（　　）

試題詳情

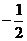
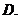
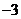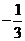
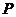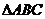高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。               高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                    高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                      高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

6．已知高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，且高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，其中高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，則高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的值有可能是（　　）

試題詳情

高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。　　　　高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。或高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。　　　　　高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。或高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。　　　　　高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。或高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

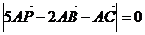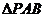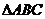7．設高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。為高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。所在平面內一點，且高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，則高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的面積與高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 的面積

比為                                                                                                                 （    ）

試題詳情

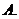
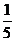
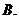
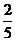
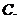
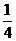
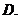
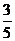
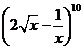高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 

試題詳情

8．二項式高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。展開式中，所有有理項（不含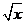高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的項）的系數之和為      （    ）

試題詳情

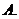
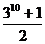
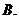
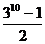
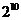
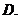
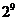
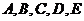     高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。             高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。             高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。                高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

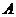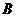9．高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。五人爭奪某項比賽的前三名，組織者對前三名發給不同的獎品，若高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。獲獎，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。不是第一名，則不同的發獎方式共有                  （    ）

試題詳情

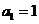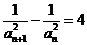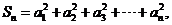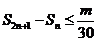
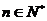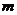       高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。72種                   高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。30種                   高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。24種                   高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。14種

試題詳情

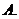
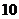
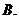
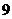
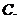
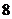
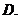
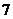
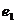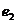10．數列高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。滿足：高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。若高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

對于任意高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。都成立，則正整數高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的最小值為( 　  )

　　　　　　　　　　　　　　　　　　　　　　　

試題詳情

高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。             　高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。          　高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。               高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

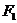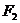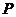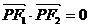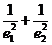11．設高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。分別為具有公共焦點高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。與高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的橢圓和雙曲線的離心率，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。為兩曲線的一個公共點，且滿足高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，則高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的值為　　　　　　　　　　（　　）

試題詳情

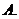
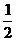
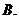
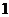
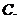
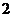
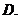
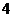
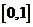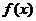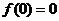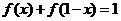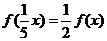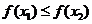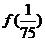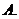
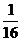
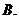
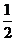
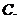
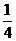
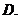
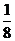
高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。      　　　高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。      　　　高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。         　　高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

12．定義在高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。上的函數高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。滿足：高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，且當高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。時，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，則高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的值為　　　　　　（    ）

試題詳情

      高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。             高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 　　　　　　　 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。              高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

 

 

 

第Ⅱ卷（非選擇題　共90分）

試題詳情

二、填空題：本大題共4小題，每小題4分，共16分.把答案填在題中橫線上.

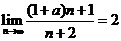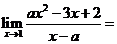13．若高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，則高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。        ；

試題詳情

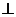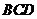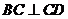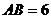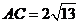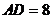14．已知點A，B，C，D在同一球面上，AB高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。平面高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，若高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，則B、C兩點間的球面距離是        ；

試題詳情

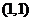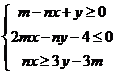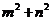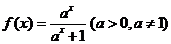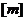15．如果點高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。在不等式組高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。所表示的平面區域內，則高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的取值范圍是   ；

試題詳情

16．設函數高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。表示不超過實數m的最大整數，則函數

試題詳情

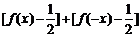高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的值域是        ．

試題詳情

三、解答題：本大題共6小題，共74分.解答應寫出文字說明，證明過程或演算步驟.

17．（本題滿分12分）

試題詳情

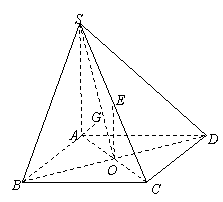
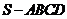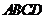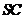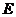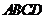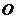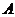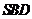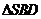已知四棱錐高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的底面高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。是正方形，側棱高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的中點高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。在底面內的射影恰好是正方形高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的中心高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，頂點高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。在截面高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。內的射影恰好是高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。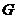的重心高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。．

試題詳情

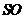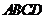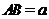高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。（1）求直線高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。與底面高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。所成角的正切值；

試題詳情

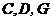（2）設高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，求此四棱錐過點高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的截面面積．

 

 

 

 

 

 

 

 

 

 

 

試題詳情

18．（本題滿分12分）

試題詳情

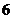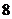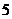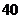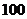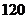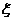某鮮花店的鮮花進價為每束高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。元，銷售價為每束高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。元．若當天沒有銷完，則以每束高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。元的價格處理掉．假如某一天該鮮花店訂購鮮花數量是高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。束、高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。束或高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。束，鮮花需求量高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的分布列是：

　　　　　　

試題詳情

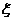高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。（束）

試題詳情

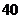
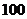
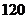
高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

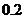
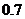
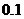
高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

p

試題詳情

高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

試題詳情

高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。

 

試問：（1）這一天鮮花需求量的期望值是多少？

（2）該花店這一天應訂購多少束鮮花盈利最大？

 

 

 

 

 

 

試題詳情

19. （本題滿分12分）

試題詳情

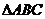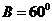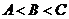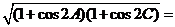
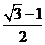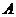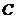在銳角高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。中，已知高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，且高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。.

試題詳情

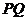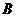（1）求角高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。與高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的大小；

試題詳情

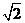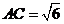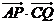（2）高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。是以高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。為圓心，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。為半徑的圓的直徑，已知高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，求高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的最大值.

　

 

 

 

 

試題詳情

20．（本題滿分12分）

試題詳情

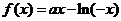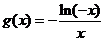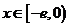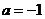已知高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。， 高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，其中高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。.

試題詳情

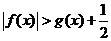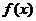(1)當高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。時，求證高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。；

試題詳情

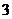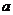(2)若高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的最小值為高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，試求高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的值.

 

 

 

 

 

 

 

試題詳情

21．（本題滿分12分）

試題詳情

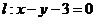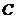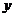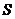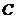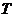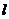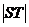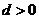已知直線高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，拋物線高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的頂點在原點，焦點在高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。軸正半軸上，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。是拋物線高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。上任意一點，高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。是直線高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。上任意一點，若高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的最小值為高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。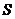時,點高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。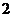的橫坐標為高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。.

試題詳情

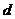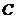（1）求拋物線方程以及高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的值；

試題詳情

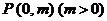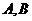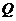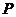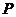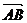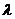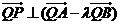（2）過拋物線高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的對稱軸上任一點高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。作直線與拋物線交于高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。兩點，點高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。是點高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。關于原點的對稱點.設點高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。分有向線段高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。所成的比為高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。，

試題詳情

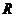證明:高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。;

試題詳情

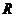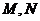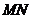（3）設高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。為拋物線準線上任意一點，過高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。作拋物線的兩條切線，切點分別為高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。,直線高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。 是否恒過一定點？若恒過定點，請指出定點；若不恒過定點，請說明理由.

 

 

 

 

試題詳情

22．（本題滿分14分）

試題詳情

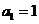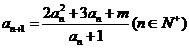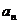已知數列高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。滿足遞推關系高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。且高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。.

試題詳情

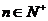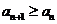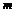（1）在高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。時，求數列高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的通項高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。；

試題詳情

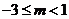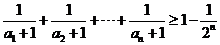(2) 當高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。時，數列高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。滿足不等式高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。恒成立，求高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。的取值范圍；

試題詳情

(3) 在高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。時，證明：高考資源網(www.uz2rxb8d2.cn)，中國最大的高考網站，您身邊的高考專家。.

 

 

 

 

 

 

 

撫州一中2009屆高三第四次模擬考試

試題詳情

一、選擇題

題號

1

2

3

4

5

6

7

8

9

10

11

12

答案

B

A

B

D

D

C

A

A

B

A

C

D

一、            填空題13.高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。；  14.高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。；  15.高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。；16.高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，即高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，當m為整數時，值為0，m為小數時，值為-1，故所求值域為{-1,0}

三、解答題

１7．（1）高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

    高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

    高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。兩兩相互垂直, 連結高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。并延長交高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。于F．

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。    高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

  高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

    同理可得高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

   高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

   高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

   高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，   高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。   ……  (6分)

（2）高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。是高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。的重心

    F是SB的中點

   高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

   高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。梯形的高

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.……  (12分)

  【注】可以用空間向量的方法.

18．（1）高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.…………4分

（2）若該天訂購高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。束鮮花，則盈利為高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。元；

若該天訂購高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。束鮮花，盈利為高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，則其分布列為

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。（元）.

若該天訂購高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。束鮮花，盈利為高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，則其分布列為

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。（元）.

綜上可知，該花店這一天應訂購高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。束鮮花盈利最大. …………12分

19．（1）高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.

又高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.………6分

（2）

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

又高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.從而

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

當高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。且同向時，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.………12分

20．（1）當高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。時，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，令高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.

列表分析：

 

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

 

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

故高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。在高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。上滿足高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，從而高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.

設高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，令高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。在高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。上為減函數，故高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，由于　高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，從而高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.……6分

（2）高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.

①若高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，則高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，令高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，矛盾.

②若高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，令高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.

 

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

 

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

 

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，令高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.

③若高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，則高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，令高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，得高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。（舍去）.

　　綜合①②③知高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.　　　……12分

21．（1）設拋物線方程為高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，

由高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。 高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

∴高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，∴拋物線方程為高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。；

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。…………4分

（2）依題意，可設直線高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。的方程為 高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。代入拋物線方程高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。得   

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。     ①

設高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。兩點的坐標分別是 高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。、高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。、高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。是方程①的兩根.…………6分

所以  高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。                                                 

由點高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。分有向線段高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。所成的比為高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，得高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

又點高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。與點高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。關于原點對稱，故點高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。的坐標是高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，從而高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。 ……7分

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。 所以  高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。  …………8分

（3）設高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，∵高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，

∴高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。的方程為高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。；

∵高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。過高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，∴高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，同理高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

∴高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。為方程高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。的兩個根；∴高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。；……11分

又高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，∴高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。的方程為高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。

∴高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，顯然直線高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。過點高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。……12分

22．（1）高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。……4分

(2)由高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，而高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。， 高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。恒成立，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，即高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。．……8分

(3) 由(2)得當高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。時知高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，設數列高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。.

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，故高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，

高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。，

即高考資源網(www.ks5u.com)，中國最大的高考網站，您身邊的高考專家。　　　　　………14分

 


同步練習冊答案
主站蜘蛛池模板： 四虎永久网址 | 欧美激情自拍偷拍 | 天堂亚洲| 亚洲v欧美 | 国产区免费观看 | 成人亚洲 | 亚洲视频一 | 久久久夜夜夜 | 国产不卡一区二区三区在线观看 | 亚洲国产婷婷香蕉久久久久久99 | 巨大黑人极品videos精品 | 欧美精品一级 | 国产精品毛片在线看 | www日韩欧美 | 在线欧美成人 | 国产黄a三级三级三级av在线看 | 精品欧美| 91视频播放 | 中文字幕一区二区不卡 | 午夜亚洲电影 | 欧美综合第一页 | 亚洲成人av在线 | 最新国产精品精品视频 | 亚洲在线| a∨在线观看 | 亚州精品成人 | 国产电影一区二区三区图片 | 国产高清在线精品一区二区三区 | 在线亚洲精品 | 欧美日b | 久久国产精品99久久久久久老狼 | 欧美高清一区 | 在线视频久久 | 国产99久久精品一区二区永久免费 | 黄色小视频免费观看 | 日韩在线亚洲 | 久久精品福利视频 | 国模精品视频一区二区 | 欧美久久综合 | 成人精品鲁一区一区二区 | 精品在线视频免费观看 |