
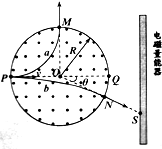
 阿爾法磁譜儀(簡稱AMS)是一個安裝于國際空間站上的粒子物理試驗設備.假設在某次探測中,觀測到從磁場邊界的左端點P沿直徑PQ垂直磁場方向射入磁場的宇宙射線中含有a和b兩種粒子,經磁場偏轉后,a、b分別從磁場邊界M、N兩點離開磁場區域,b與電磁量能器的撞擊點為S,如圖所示.已知a、b的入射速度大小分別為v1、v2,圖形磁場半徑為R,O為圓心,磁場方向垂直紙面向外,磁感應強度大小B,OM⊥PQ,∠QON=θ,不考慮粒子間相互作用和相對論效應.
阿爾法磁譜儀(簡稱AMS)是一個安裝于國際空間站上的粒子物理試驗設備.假設在某次探測中,觀測到從磁場邊界的左端點P沿直徑PQ垂直磁場方向射入磁場的宇宙射線中含有a和b兩種粒子,經磁場偏轉后,a、b分別從磁場邊界M、N兩點離開磁場區域,b與電磁量能器的撞擊點為S,如圖所示.已知a、b的入射速度大小分別為v1、v2,圖形磁場半徑為R,O為圓心,磁場方向垂直紙面向外,磁感應強度大小B,OM⊥PQ,∠QON=θ,不考慮粒子間相互作用和相對論效應.分析 (1)由左手定則從a粒子的偏轉方向就能判斷a粒子的電性.由于從M點射出,粒子偏轉90°,時間為四分之一周期.
(2)由b粒子的偏轉角和幾何關系求出b粒子做勻速圓周運動的半徑,再由洛侖茲力提供向心力就能求得b粒子的比荷.
(3)電磁量能器測得粒子b撞擊時的能量為E,該能量為b粒子的動能.由動能公式和前面已經求得的比荷,從而就能求出粒子的電荷量.
解答 解:(1)根據左手定則,粒子a帶負電,粒子a從P點進入至M點離開磁場的過程中,偏轉了90°角,設運動時間為t,則有:
t=$\frac{1}{4}$T
粒子做圓周運動的周期$T=\frac{2π{r}_{a}}{{v}_{1}}$
由幾何關系,粒子a在磁場中做圓周運動的半徑ra=R
聯立方程得:t=$\frac{πR}{2{v}_{1}}$
(2)由幾何關系得,粒子b在磁場中做圓周運動的半徑
${r}_{b}=\frac{R}{tan\frac{θ}{2}}$
洛倫茲力提供向心力:qvB=m$\frac{v2}{r}$
即:r=$\frac{mv}{qB}$
所以,粒子b的荷質比
$\frac{q}{m}=\frac{{v}_{2}tan\frac{θ}{2}}{BR}$
(3)粒子b撞擊電磁量能器的能量E為粒子的動能,即:
$E=\frac{1}{2}m{{v}_{2}}^{2}$
所以粒子b的質量為:$m=\frac{2E}{{{v}_{2}}^{2}}$
由(2)結論可得,粒子b所帶電量為:
$q=\frac{2Etan\frac{θ}{2}}{BR{v}_{2}}$
答:(1)粒子a的電性是帶負電,其在磁場中運動的時間為$\frac{πR}{2{v}_{1}}$.
(2)粒子b的荷質比為$\frac{{v}_{2}tan\frac{θ}{2}}{BR}$.
(3)若電磁量能器測得粒子b撞擊時的能量為E,b所帶電量為$\frac{2Etan\frac{θ}{2}}{BR{v}_{2}}$.
點評 本題涉及阿爾法磁譜儀的工作過程,想象中有兩個粒子以相同的能量進入該儀器.分別打在不同位置,根據題設來探測粒子的電性和粒子的比荷.該類問題屬簡單的帶電粒子在圓形磁場區域內做勻速圓周運動問題,由幾何關系和牛頓第二定律可以解決問題.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:高中物理 來源: 題型:多選題
| A. | 一定沿電場線運動 | B. | 一定由高電勢處向低電勢處運動 | ||
| C. | 不一定沿電場線運動 | D. | 不一定由高電勢處向低電勢處運動 |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
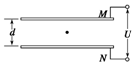 如圖所示,平行板電容器兩極板M、N相距d,兩極板分別與電壓恒定為U的電源兩極連接,極板M帶正電.現有一質量為m的帶電油滴在極板中央處于靜止狀態,則( )
如圖所示,平行板電容器兩極板M、N相距d,兩極板分別與電壓恒定為U的電源兩極連接,極板M帶正電.現有一質量為m的帶電油滴在極板中央處于靜止狀態,則( )| A. | 油滴帶負電 | |
| B. | 油滴帶正電 | |
| C. | 油滴帶電荷量為$\frac{mgd}{U}$ | |
| D. | 將極板N向下緩慢移動一小段距離,油滴將向上運動 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
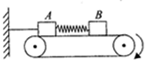 如圖所示,兩個質量分別為m1、m2的物塊A和B通過一輕彈簧連接在一起并放置于水平傳送帶上,水平輕繩一端連接A,另一端固定在墻上,A、B與傳送帶間動摩擦因數均為μ.傳送帶順時針方向轉動,系統達到穩定后,突然剪斷輕繩的瞬間,設A、B的加速度大小分別為aA和aB,(彈簧在彈性限度內,重力加速度為g)則( )
如圖所示,兩個質量分別為m1、m2的物塊A和B通過一輕彈簧連接在一起并放置于水平傳送帶上,水平輕繩一端連接A,另一端固定在墻上,A、B與傳送帶間動摩擦因數均為μ.傳送帶順時針方向轉動,系統達到穩定后,突然剪斷輕繩的瞬間,設A、B的加速度大小分別為aA和aB,(彈簧在彈性限度內,重力加速度為g)則( )| A. | aA=μ(1+$\frac{{m}_{2}}{{m}_{1}}$)g,aB=μg | B. | aA=μg,aB=0 | ||
| C. | aA=μ(1+$\frac{{m}_{2}}{{m}_{1}}$)g,aB=0 | D. | aA=μg,aB=μg |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
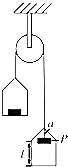 如圖所示,輕質滑輪兩邊分別用細繩懸掛托盤和小重物,每個托盤和小重物的質量均為m,開始托盤和小重物靜止,右邊小重物P被細繩a懸掛且距離盤底的距離為l,如果某時刻重物P由于細繩a斷裂下落,重力加速度為g.
如圖所示,輕質滑輪兩邊分別用細繩懸掛托盤和小重物,每個托盤和小重物的質量均為m,開始托盤和小重物靜止,右邊小重物P被細繩a懸掛且距離盤底的距離為l,如果某時刻重物P由于細繩a斷裂下落,重力加速度為g.查看答案和解析>>
科目:高中物理 來源: 題型:多選題
 如圖所示,一理想變壓器原線圈匝數n1=1100匝,副線圈匝數n2=110匝,交流電源的電壓u=220$\sqrt{2}$sin100πtV,電壓表、電流表均為理想電表,單刀雙擲開關開始接a,則以下說法正確的是( )
如圖所示,一理想變壓器原線圈匝數n1=1100匝,副線圈匝數n2=110匝,交流電源的電壓u=220$\sqrt{2}$sin100πtV,電壓表、電流表均為理想電表,單刀雙擲開關開始接a,則以下說法正確的是( )| A. | 交流電的頻率為50Hz | |
| B. | 電壓表的示數為22$\sqrt{2}$V | |
| C. | 當開關由a撥至b時,電流表示數變小 | |
| D. | 當開關由a撥至b時,穿過副線圈的磁通量變化率變大 |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
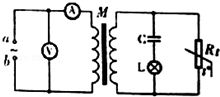 某一火警報警系統原理圖如圖所示,報警器未畫出,a、b接在電壓u=311sin314t(V)的正弦交流電源上,Rt為半導體熱敏材料制成的傳感器,Rt的電阻值隨溫度升高而減小,下列說法正確的是( )
某一火警報警系統原理圖如圖所示,報警器未畫出,a、b接在電壓u=311sin314t(V)的正弦交流電源上,Rt為半導體熱敏材料制成的傳感器,Rt的電阻值隨溫度升高而減小,下列說法正確的是( )| A. | 電壓表V的示數為220V | |
| B. | 電容器C電容增大,燈L變暗 | |
| C. | Rt所在處出現火警時,電流表A的示數增大 | |
| D. | Rt所在處出現火警時,變壓器輸入功率減小 |
查看答案和解析>>
科目:高中物理 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com