

分析 由圖象可以看出根彈簧的伸長量X與所受拉力F是線性關系,解出斜率即能找到圖線對應的函數,根據胡克定律可以解出彈簧的勁度系數,以及已知拉力時彈簧的形變量.
解答 解:(1)由圖象可以解出傾斜直線的斜率,由圖可知,當拉力為800N時,形變量為x=40cm=0.4m;則有:
k=$\frac{△F}{△x}$=$\frac{800-0}{0.4}$=2000N/m
由于F=kx
解得:F=2000x
(2)根據胡克定律彈簧的彈力與彈簧的形變量成正比,比例系數即為彈簧的勁度系數;所以彈簧的勁度系數為2000N/m.
(3)由圖可知,當彈簧受F2=800N的拉力作用時,形變量為40cm;
故答案為:(1)F=2000x,(2)2000;(3)40.
點評 胡克定律的應用注意形變量x既可以是彈簧的伸長量,也可以是彈簧的壓縮量;還要注意胡克定律適用的條件為形變量應在彈性限度內.


科目:高中物理 來源: 題型:實驗題

查看答案和解析>>
科目:高中物理 來源: 題型:多選題
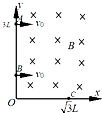 如圖所示,在xoy平面的第Ⅰ象限內存在垂直xoy平面向里、磁感應強度大小為B的勻強磁場,兩個相同的帶電粒子以相同的速度v0先后從y軸上坐標(0,3L)的A點和B點(坐標未知)垂直于y軸射入磁場,在x軸上坐標($\sqrt{3}$L,0)的C點相遇,不計粒子重力及其相互作用.根據題設條件可以確定( )
如圖所示,在xoy平面的第Ⅰ象限內存在垂直xoy平面向里、磁感應強度大小為B的勻強磁場,兩個相同的帶電粒子以相同的速度v0先后從y軸上坐標(0,3L)的A點和B點(坐標未知)垂直于y軸射入磁場,在x軸上坐標($\sqrt{3}$L,0)的C點相遇,不計粒子重力及其相互作用.根據題設條件可以確定( )| A. | 帶電粒子在磁場中運動的半徑 | B. | B點的位置坐標為$\frac{L}{2}$ | ||
| C. | 兩個帶電粒子在磁場中運動的時間 | D. | 帶電粒子的質量 |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
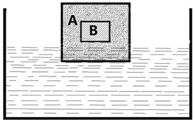 有一實心立方體A,邊長為L,從內部去掉一部分物質,剩余部分質量為m,一立方體B恰能完全填充A的空心部分,質量也為m,如圖所示,即B的外表面與A的內表面恰好接觸.整體放在一個盛有密度為ρ的液體的容器里(容器無限大),剛開始,A漂浮在液面上,用外力使A向下產生位移b,平衡后由靜止釋放,A將要上下振動(水的摩擦阻力不計).可以證明該振動為簡諧運動,振動過程中,A始終不離開液面,也不被液面埋沒,已知重力加速度g求:
有一實心立方體A,邊長為L,從內部去掉一部分物質,剩余部分質量為m,一立方體B恰能完全填充A的空心部分,質量也為m,如圖所示,即B的外表面與A的內表面恰好接觸.整體放在一個盛有密度為ρ的液體的容器里(容器無限大),剛開始,A漂浮在液面上,用外力使A向下產生位移b,平衡后由靜止釋放,A將要上下振動(水的摩擦阻力不計).可以證明該振動為簡諧運動,振動過程中,A始終不離開液面,也不被液面埋沒,已知重力加速度g求:查看答案和解析>>
科目:高中物理 來源: 題型:解答題
查看答案和解析>>
科目:高中物理 來源: 題型:計算題
 如圖所示是傾角θ=37°的固定光滑斜面,兩端有垂直于斜面的固定擋板P、Q,PQ距離L=3m,質量M=2.0kg的木塊A(可看成質點)放在質量m=0.5kg 的長d=1.2m的木板B上并一起停靠在擋板P處,A木塊與斜面頂端的電動機間用平行于斜面不可伸長的輕繩相連接,現給木塊A沿斜面向上的初速度,同時開動電動機保證木塊A一直以初速度v0=4m/s沿斜面向上做勻速直線運動,已知木塊A的下表面與木板B間動摩擦因數μ1=0.5,經過時間t,當B板右端到達Q處時刻,立刻關閉電動機,同時鎖定A、B物體此時的位置.然后將A物體上下面翻轉,使得A原來的上表面與木板B接觸,已知翻轉后的A、B接觸面間的動摩擦因數變為μ2=0.125,且連接A與電動機的繩子仍與斜面平行.現在給A向下的初速度v1=4m/s,同時釋放木板B,并開動電動機保證A木塊一直以v1沿斜面向下做勻速直線運動,直到木板B與擋板P接觸時關閉電動機并鎖定A、B位置.(g=10m/s2.$\sqrt{5}$=2.24)求:
如圖所示是傾角θ=37°的固定光滑斜面,兩端有垂直于斜面的固定擋板P、Q,PQ距離L=3m,質量M=2.0kg的木塊A(可看成質點)放在質量m=0.5kg 的長d=1.2m的木板B上并一起停靠在擋板P處,A木塊與斜面頂端的電動機間用平行于斜面不可伸長的輕繩相連接,現給木塊A沿斜面向上的初速度,同時開動電動機保證木塊A一直以初速度v0=4m/s沿斜面向上做勻速直線運動,已知木塊A的下表面與木板B間動摩擦因數μ1=0.5,經過時間t,當B板右端到達Q處時刻,立刻關閉電動機,同時鎖定A、B物體此時的位置.然后將A物體上下面翻轉,使得A原來的上表面與木板B接觸,已知翻轉后的A、B接觸面間的動摩擦因數變為μ2=0.125,且連接A與電動機的繩子仍與斜面平行.現在給A向下的初速度v1=4m/s,同時釋放木板B,并開動電動機保證A木塊一直以v1沿斜面向下做勻速直線運動,直到木板B與擋板P接觸時關閉電動機并鎖定A、B位置.(g=10m/s2.$\sqrt{5}$=2.24)求:查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
 (1)在探究求合力的方法時,先將橡皮條的一端固定在水平木板上,另一端系上帶有繩套的兩根細繩.實驗時,需要兩次拉伸橡皮條,一次是通過兩細繩用兩個彈簧秤互成角度地拉橡皮條,另一次是用一個彈簧秤通過細繩拉橡皮條.
(1)在探究求合力的方法時,先將橡皮條的一端固定在水平木板上,另一端系上帶有繩套的兩根細繩.實驗時,需要兩次拉伸橡皮條,一次是通過兩細繩用兩個彈簧秤互成角度地拉橡皮條,另一次是用一個彈簧秤通過細繩拉橡皮條.查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | $\frac{kQq}{2a}$ | B. | -$\frac{kQq}{2a}$ | C. | -$\frac{kQq}{2({a}^{2}-{c}^{2})}$ | D. | -$\frac{kQq}{2c}$ |
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
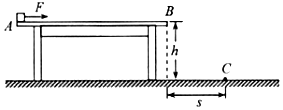 如圖所示,水平桌面AB離地高度為h=1.25m,AB兩端間距為L=3.2m,物塊在F=20N的水平拉力作用下從A端由靜止開始運動,拉力F作用一段時間后撤去.已知該物塊可視為質點,質量m=2.0kg,與水平桌面的動摩擦因數μ=0.5,水平地面上的C點到桌面B端的水平距離為s=1.0m,取g=10m/s2.
如圖所示,水平桌面AB離地高度為h=1.25m,AB兩端間距為L=3.2m,物塊在F=20N的水平拉力作用下從A端由靜止開始運動,拉力F作用一段時間后撤去.已知該物塊可視為質點,質量m=2.0kg,與水平桌面的動摩擦因數μ=0.5,水平地面上的C點到桌面B端的水平距離為s=1.0m,取g=10m/s2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com