
分析 根據萬有引力提供向心力求出衛星在半徑為r1圓形軌道運動的速度,從而知道動能,通過引力勢能公式求出在軌道r1上的機械能,同理可以求出衛星在軌道r2上的機械能,衛星的圓軌道半徑從r1逐漸減小到r2.在這個過程中空氣阻力做功Wf等于衛星機械能的變化量.
解答 解:衛星在圓軌道半徑r1上運行時,根據萬有引力提供向心力得:G$\frac{Mm}{{r}_{1}^{2}}$=m$\frac{{v}_{1}^{2}}{{r}_{1}}$
得 v1=$\sqrt{\frac{GM}{{r}_{1}}}$
所以衛星的動能為 Ek1=$\frac{1}{2}$mv12=$\frac{GMm}{2{r}_{1}}$.
衛星的總機械能:E1=Ek1+Ep1=$\frac{GMm}{2{r}_{1}}$-$\frac{GMm}{{r}_{1}}$=-$\frac{GMm}{2{r}_{1}}$.
同理:衛星的圓軌道半徑從r2上時,動能為 Ek2=$\frac{GMm}{2{r}_{2}}$
衛星的總機械能:E2=-$\frac{GMm}{2{r}_{2}}$
衛星的圓軌道半徑從r1逐漸減小到r2.在這個過程中空氣阻力做功Wf等于衛星機械能的變化量,則有:Wf=E2-E1=$\frac{GMm}{2{r}_{1}}$-$\frac{GMm}{2{r}_{2}}$.
故答案為:$\frac{GMm}{2{r}_{1}}$-$\frac{GMm}{2{r}_{2}}$.
點評 解決本題的關鍵得出衛星動能和勢能的和即機械能的變化量,從而空氣阻力做功為Wf等于衛星機械能的變化量這個功能關系計算.


科目:高中物理 來源: 題型:計算題
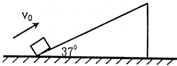 質量m=1kg物體,以v0=20m/s的初速度滑上一傾角為θ=37°的固定斜面,經2s到在最高點后又沿斜面滑下.以下兩小題中距離和速度請用動能定理求解(g取10m/s2)
質量m=1kg物體,以v0=20m/s的初速度滑上一傾角為θ=37°的固定斜面,經2s到在最高點后又沿斜面滑下.以下兩小題中距離和速度請用動能定理求解(g取10m/s2)查看答案和解析>>
科目:高中物理 來源: 題型:填空題
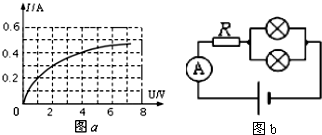
查看答案和解析>>
科目:高中物理 來源: 題型:填空題
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
| A. | 該衛星可能是通過地球兩極上方的軌道 | |
| B. | 該衛星平面可能與南緯30○ 52′所確定的平面共面 | |
| C. | 該衛星平面一定與東經115○ 52′所確定的平面共面 | |
| D. | 地球自轉周期一定是該衛星運行周期的整數倍 |
查看答案和解析>>
科目:高中物理 來源: 題型:計算題
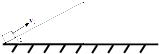 如圖所示,斜劈固定放置在水平地面上,它的斜面長度L=3.4m,傾角為α=30°.從某時刻起,一木塊(可視為質點)以v0=10m/s的初速度從斜面底端沿平行斜面方向沖上斜面,木塊與斜面間的動摩擦因數$μ=\frac{{\sqrt{3}}}{2}$,空氣阻力不計,重力加速度g取10m/s2.求木塊沖出斜面后剛接觸地面時的速率v.
如圖所示,斜劈固定放置在水平地面上,它的斜面長度L=3.4m,傾角為α=30°.從某時刻起,一木塊(可視為質點)以v0=10m/s的初速度從斜面底端沿平行斜面方向沖上斜面,木塊與斜面間的動摩擦因數$μ=\frac{{\sqrt{3}}}{2}$,空氣阻力不計,重力加速度g取10m/s2.求木塊沖出斜面后剛接觸地面時的速率v.查看答案和解析>>
科目:高中物理 來源: 題型:計算題
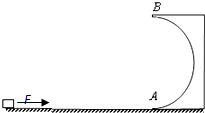 半徑為R=0.9m的光滑半圓形軌道固定在水平地面上,與水平面相切于A點,在距離A點1.3m處有一可視為質點的小滑塊,質量為m=0.5kg,小滑塊與水平面間的動摩擦因數為u=0.2,施加一個大小為F=11N的水平推力,運動到A點撤去推力,滑塊從圓軌道最低點A處沖上豎直軌道.(g=10m/s2)問:
半徑為R=0.9m的光滑半圓形軌道固定在水平地面上,與水平面相切于A點,在距離A點1.3m處有一可視為質點的小滑塊,質量為m=0.5kg,小滑塊與水平面間的動摩擦因數為u=0.2,施加一個大小為F=11N的水平推力,運動到A點撤去推力,滑塊從圓軌道最低點A處沖上豎直軌道.(g=10m/s2)問:查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 質量小的物體一定能視為質點 | |
| B. | 體積小的物體一定能視為質點 | |
| C. | 研究地球自轉時能把地球視為質點 | |
| D. | 研究地球繞太陽公轉時能把地球視為質點 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 研究乒乓球的旋轉 | B. | 研究流星的墜落軌跡 | ||
| C. | 研究運動員的跨欄動作 | D. | 研究蝴蝶翅膀的振動 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com