
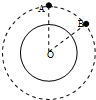
 如圖所示,一衛星在某一軌道上繞地心O做勻速圓周運動,軌道半徑為r.經過時間t該衛星從位置A運行到位置B,∠AOB=60°.設地球半徑為R,地球表面重力加速度為g.則下列說法中正確的是( )
如圖所示,一衛星在某一軌道上繞地心O做勻速圓周運動,軌道半徑為r.經過時間t該衛星從位置A運行到位置B,∠AOB=60°.設地球半徑為R,地球表面重力加速度為g.則下列說法中正確的是( )| A. | 衛星的加速度為$\frac{{R}^{2}g}{{r}^{2}}$ | |
| B. | 在衛星返回地面的過程中萬有引力減弱重力增大 | |
| C. | 衛星由位置A運動到位置B需要的時間為$\frac{πr}{3R}$$\sqrt{\frac{r}{g}}$ | |
| D. | 衛星由位置A運動到位置B的過程中萬有引力做功為零 |
分析 在地球表面重力與萬有引力相等,萬有引力提供衛星圓周運動的向心力,衛星通過做近心運動或離心運動來實現軌道位置的調整.
解答 解:A、在地球表面重力與萬有引力相等,在衛星處萬有引力提供圓周運動向心力,故有:
$G\frac{Mm}{{R}_{\;}^{2}}=mg$,$G\frac{Mm}{{r}_{\;}^{2}}=ma$,由兩式可得兩顆衛星的加速度大小均為$a=\frac{g{R}_{\;}^{2}}{{r}_{\;}^{2}}$,故A正確;
B、衛星在返回地面的過程中,與地心的距離減小,根據萬有引力定律$F=G\frac{Mm}{{r}_{\;}^{2}}$,知萬有引力增大,越靠近地球表面重力加速度越大,重力越大,故B錯誤;
C、由A知,衛星的向心加速度a=$\frac{{R}_{\;}^{2}}{{r}_{\;}^{2}}g$=$\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$,可得衛星的周期$T=2π\frac{r}{R}\sqrt{\frac{r}{g}}$,所以從A運動到B所用時間t=$\frac{60°}{360°}T=\frac{πr}{3R}\sqrt{\frac{r}{g}}$,故C正確;
D、衛星1做勻速圓周運動萬有引力提供圓周運動向心力,即引力始終與速度方向垂直,故萬有引力對衛星不做功,故D正確.
故選:ACD.
點評 本題主要考查了萬有引力應用問題,掌握星球表面重力與萬有引力相等,環繞天體繞中心天體圓周運動萬有引力提供向心力.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:高中物理 來源: 題型:計算題
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
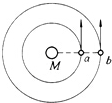 如圖,a和b是某天體M的兩個衛星,它們繞天體公轉的周期為Ta和Tb,某一時刻兩衛星運動至圖示位置,且公轉方向相同.
如圖,a和b是某天體M的兩個衛星,它們繞天體公轉的周期為Ta和Tb,某一時刻兩衛星運動至圖示位置,且公轉方向相同.查看答案和解析>>
科目:高中物理 來源: 題型:填空題
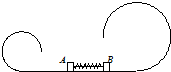 如圖所示,一光滑軌道由水平軌道和圓弧形軌道構成,放在豎直平面內,圓弧形軌道半徑分別為R和2R,在水平軌道上有A、B兩物體,A、B中間隔有一輕彈簧,用細線連接A、B并使輕彈簧處于壓縮狀態.若剪斷細線,A、B兩物體能分別運動到左右兩圓弧形軌道的最高點,且對軌道壓力都為零.若不計任何摩擦,則A、B兩物體的質量mA和mB之比為$\sqrt{2}$:1.
如圖所示,一光滑軌道由水平軌道和圓弧形軌道構成,放在豎直平面內,圓弧形軌道半徑分別為R和2R,在水平軌道上有A、B兩物體,A、B中間隔有一輕彈簧,用細線連接A、B并使輕彈簧處于壓縮狀態.若剪斷細線,A、B兩物體能分別運動到左右兩圓弧形軌道的最高點,且對軌道壓力都為零.若不計任何摩擦,則A、B兩物體的質量mA和mB之比為$\sqrt{2}$:1.查看答案和解析>>
科目:高中物理 來源: 題型:解答題
查看答案和解析>>
科目:高中物理 來源: 題型:計算題
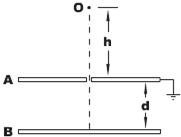 如圖所示,水平放置的兩平行金屬板A、B構成電容器,電容為C,極板間距為d,開始時兩板均不帶電,讓帶有小孔的A板接地.在A板小孔的正上方高h的O點有帶電油滴一滴一滴地滴下,已知油滴每滴的質量為m,電量為q,且每滴落到B板后,都會將電荷全部傳給B板(A板的下表面也會同時感應出等量的異種電荷),空氣阻力不計.求:
如圖所示,水平放置的兩平行金屬板A、B構成電容器,電容為C,極板間距為d,開始時兩板均不帶電,讓帶有小孔的A板接地.在A板小孔的正上方高h的O點有帶電油滴一滴一滴地滴下,已知油滴每滴的質量為m,電量為q,且每滴落到B板后,都會將電荷全部傳給B板(A板的下表面也會同時感應出等量的異種電荷),空氣阻力不計.求:查看答案和解析>>
科目:高中物理 來源: 題型:計算題
 如圖,ABCD為一豎直平面的軌道,其中BC水平,A點比BC高出10米,BC長1米,AB和CD軌道光滑.一質量為1千克的物體,從A點以4米/秒的速度開始運動,經過BC后滑到高出C點10.3m的D點速度為零.求:(g=10m/s2)
如圖,ABCD為一豎直平面的軌道,其中BC水平,A點比BC高出10米,BC長1米,AB和CD軌道光滑.一質量為1千克的物體,從A點以4米/秒的速度開始運動,經過BC后滑到高出C點10.3m的D點速度為零.求:(g=10m/s2)查看答案和解析>>
科目:高中物理 來源: 題型:多選題
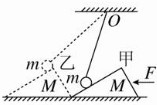 如圖所示,小球m用一條不可伸長的輕質細線拴住后懸于O點,小球置于一個斜面不光滑的斜劈M上,用水平力F向左推動斜劈M在光滑水平桌面上由位置甲向左緩慢移動到位置乙,在此過程中,正確的說法是( )
如圖所示,小球m用一條不可伸長的輕質細線拴住后懸于O點,小球置于一個斜面不光滑的斜劈M上,用水平力F向左推動斜劈M在光滑水平桌面上由位置甲向左緩慢移動到位置乙,在此過程中,正確的說法是( )| A. | M、m間的摩擦力對m不做功 | |
| B. | M、m間的摩擦力對m做負功 | |
| C. | F對M所做的功與m對M所做的功的絕對值相等 | |
| D. | M、m間的彈力對m做正功 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com