
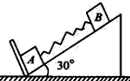
 在傾角為30°的足夠長的光滑斜面底端固定一個垂直于斜面的擋板,物體A,B用輕彈簧連接并放在斜面上,系統處于靜止狀態,如圖所示,已知物體A的質量mA=2kg,物體B的質量mB=1kg,彈簧的勁度系數為k=100N/m,現在將物體B從靜止狀態沿斜面向下壓10cm后釋放,g取10m/s2,則在物體B運動的過程中
在傾角為30°的足夠長的光滑斜面底端固定一個垂直于斜面的擋板,物體A,B用輕彈簧連接并放在斜面上,系統處于靜止狀態,如圖所示,已知物體A的質量mA=2kg,物體B的質量mB=1kg,彈簧的勁度系數為k=100N/m,現在將物體B從靜止狀態沿斜面向下壓10cm后釋放,g取10m/s2,則在物體B運動的過程中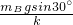 =5cm.
=5cm.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中物理 來源: 題型:
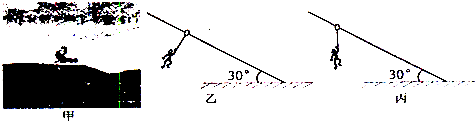
 (2009?鹽城一模)如圖甲所示,在傾角為30°的足夠長的光滑斜面上,有一質量為m的物體,受到沿斜面方向的力F作用,力F按圖乙所示規律變化(圖中縱坐標是F與mg的比值,力沿斜面向上為正).則物體運動的速度v隨時間t變化的規律是下圖中的(物體的初速度為零,重力加速度取10m/s2)( )
(2009?鹽城一模)如圖甲所示,在傾角為30°的足夠長的光滑斜面上,有一質量為m的物體,受到沿斜面方向的力F作用,力F按圖乙所示規律變化(圖中縱坐標是F與mg的比值,力沿斜面向上為正).則物體運動的速度v隨時間t變化的規律是下圖中的(物體的初速度為零,重力加速度取10m/s2)( )查看答案和解析>>
科目:高中物理 來源: 題型:
查看答案和解析>>
科目:高中物理 來源: 題型:

查看答案和解析>>
科目:高中物理 來源: 題型:
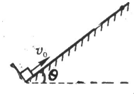 在傾角為θ=30°的足夠長的斜面底端,木塊A以某一初速度v0沿斜面向上運動,若木塊與斜面間的動摩擦因數μ=
在傾角為θ=30°的足夠長的斜面底端,木塊A以某一初速度v0沿斜面向上運動,若木塊與斜面間的動摩擦因數μ=| 1 | ||
2
|
查看答案和解析>>
科目:高中物理 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com