
 如圖所示為一繞地球運行的人造地球衛星運行軌跡,衛星近地點P近似認為貼近地球表面,遠地點Q距地面的高度為h,已知地球半徑為R,地球表面重力加速度為g,則( )
如圖所示為一繞地球運行的人造地球衛星運行軌跡,衛星近地點P近似認為貼近地球表面,遠地點Q距地面的高度為h,已知地球半徑為R,地球表面重力加速度為g,則( )| A. | 該衛星的運動周期為2π$\sqrt{\frac{(R+\frac{h}{2})^{2}}{g{R}^{2}}}$ | |
| B. | 該衛星的發射速度大于第一宇宙速度 | |
| C. | 該衛星在P點的速度大小為$\sqrt{gR}$ | |
| D. | 該衛星在P點的加速度大于地球表面的重力加速度g |
分析 求出衛星橢圓軌道的半長軸,抓住橢圓的周期與圓軌道半徑等于半長軸的周期相等,結合萬有引力提供向心力求出周期.在P點,衛星的速度大于第一宇宙速度,做離心運動.根據牛頓第二定律,結合萬有引力等于重力比較衛星在P點的加速度與地球表面重力加速度的大小關系.
解答 解:A、近地衛星的周期為${T}_{0}^{\;}$,由$mg=m\frac{4{π}_{\;}^{2}}{{T}_{0}^{2}}R$,得${T}_{0}^{\;}=2π\sqrt{\frac{{R}_{\;}^{3}}{GM}}$=$2π\sqrt{\frac{{R}_{\;}^{3}}{g{R}_{\;}^{2}}}=2π\sqrt{\frac{R}{g}}$,圖示衛星的周期為T,半長軸為$r=(R+\frac{h}{2})$,由開普勒第三定律得$\frac{{R}_{\;}^{3}}{{T}_{0}^{2}}=\frac{{r}_{\;}^{3}}{{T}_{\;}^{2}}$,解得$T=2π\sqrt{\frac{(g+\frac{h}{2})_{\;}^{3}}{g{R}_{\;}^{2}}}$,故A正確;
C、因衛星的軌道為橢圓,故衛星的發射速度大于$\sqrt{gR}$,故C錯誤;
B、發射速度大于第一宇宙速度,故B正確;
D、由萬有引力定律和牛頓第二定律知衛星在P點的加速度在P點,加速度a=$\frac{G\frac{Mm}{{R}_{\;}^{2}}}{m}=\frac{GM}{{R}_{\;}^{2}}$,地球表面的重力加速度g=$\frac{GM}{{R}_{\;}^{2}}$,即P點加速度等于地球表面的重力加速度,故D錯誤;
故選:AB
點評 解決本題的關鍵掌握萬有引力提供向心力這一重要理論,運用開普勒第三定律必須對于同一個中心天體.


科目:高中物理 來源: 題型:選擇題
| A. | 庫侖用扭秤測出了萬有引力常量 | |
| B. | 牛頓通過理想斜面實驗發現了物體的運動不需要力來維持 | |
| C. | 法拉第通過實驗發現了電磁感應現象 | |
| D. | 奧斯特通過實驗發現了電流的熱效應 |
查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
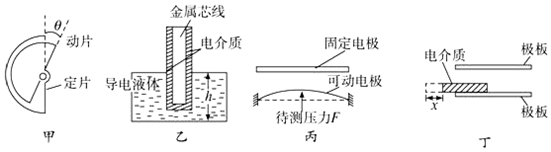
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 15 m/s2 | B. | 20 m/s2 | C. | 25 m/s2 | D. | 0m/s2 |
查看答案和解析>>
科目:高中物理 來源: 題型:實驗題

查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
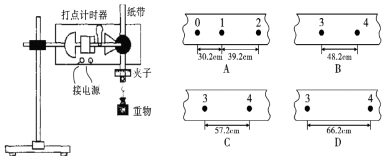
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
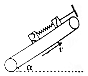 如圖所示,傾角為α的傳送帶上有質量均為m的兩個木塊1、2,它們之間用原長為L、勁度系數為k的輕彈簧連接起來,木塊與傳送帶間的動摩擦因數均為μ,其中木塊1被與傳送帶平行的細線拉住,傳動帶按圖示方向勻速運動,兩個木塊均處于平衡狀態.求:
如圖所示,傾角為α的傳送帶上有質量均為m的兩個木塊1、2,它們之間用原長為L、勁度系數為k的輕彈簧連接起來,木塊與傳送帶間的動摩擦因數均為μ,其中木塊1被與傳送帶平行的細線拉住,傳動帶按圖示方向勻速運動,兩個木塊均處于平衡狀態.求:查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
 如圖所示,彈簧的一端固定在豎直墻上,質量為M 的光滑弧形槽靜止在光滑水平面上,底部與水平面平滑連接,一個質量為m(m<M)的小球從槽高h 處開始自由下滑,下列說法正確的是( )
如圖所示,彈簧的一端固定在豎直墻上,質量為M 的光滑弧形槽靜止在光滑水平面上,底部與水平面平滑連接,一個質量為m(m<M)的小球從槽高h 處開始自由下滑,下列說法正確的是( )| A. | 在以后的運動過程中,小球和槽的水平方向動量始終守恒 | |
| B. | 被彈簧反彈后,小球和槽的機械能守恒,但小球不能回到槽高h處 | |
| C. | 全過程小球和槽、彈簧所組成的系統機械能守恒,且水平方向動量守恒 | |
| D. | 在下滑過程中小球和槽之間的相互作用力始終不做功? |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
 木塊 A、B 分別重 50N 和 30N,它們與水平地面之間的動摩擦因數均為 0.2.與 A、B 相連接的輕彈簧被壓縮了 5cm,系統置于水平地面上靜止不動.已知彈 簧的勁度系數為 100N/m.用 F=1N 的水平力作用在木塊 A 上,如圖所示,力 F 作用后( )
木塊 A、B 分別重 50N 和 30N,它們與水平地面之間的動摩擦因數均為 0.2.與 A、B 相連接的輕彈簧被壓縮了 5cm,系統置于水平地面上靜止不動.已知彈 簧的勁度系數為 100N/m.用 F=1N 的水平力作用在木塊 A 上,如圖所示,力 F 作用后( )| A. | 木塊 A 所受摩擦力大小是 4 N,方向向右 | |
| B. | 木塊 A 所受摩擦力大小是 5 N,方向向右 | |
| C. | 木塊 B 所受摩擦力大小是 4 N,方向向左 | |
| D. | 木塊 B 所受摩擦力大小是 5 N,方向向左 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com