
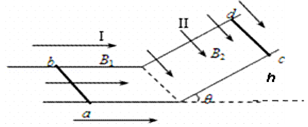
 如圖所示,傾斜角θ=30°的光滑傾斜導體軌道(足夠長)與光滑水平導體軌道連接.軌道寬度均為L=1m,電阻忽略不計.勻強磁場I僅分布在水平軌道平面所在區(qū)域,方向水平向右,大小B1=1T;勻強磁場II僅分布在傾斜軌道平面所在區(qū)域,方向垂直于傾斜軌道平面向下,大小B2=1T.現(xiàn)將兩質(zhì)量均為m=0.2kg,電阻均為R=0.5Ω的相同導體棒ab和cd,垂直于軌道分別置于水平軌道上和傾斜軌道上,并同時由靜止釋放.取g=10m/s2.
如圖所示,傾斜角θ=30°的光滑傾斜導體軌道(足夠長)與光滑水平導體軌道連接.軌道寬度均為L=1m,電阻忽略不計.勻強磁場I僅分布在水平軌道平面所在區(qū)域,方向水平向右,大小B1=1T;勻強磁場II僅分布在傾斜軌道平面所在區(qū)域,方向垂直于傾斜軌道平面向下,大小B2=1T.現(xiàn)將兩質(zhì)量均為m=0.2kg,電阻均為R=0.5Ω的相同導體棒ab和cd,垂直于軌道分別置于水平軌道上和傾斜軌道上,并同時由靜止釋放.取g=10m/s2.分析 由左、右手定則知道,當cd棒下滑時產(chǎn)生由d向c的電流,而ab棒受到豎直向下的安培力,這樣ab棒始終靜止在水平軌道上.
(1)下滑過程中當cd受到的合力為零時,速度達到最大,結(jié)合E=BLv,歐姆定律、安培力公式代入平衡條件就能求出最大速度.
(2)由能量守恒定律可以求出減少的機械能,從而減少的重力勢能求出,下滑的距離x也求出,磁通量的變化量求出,用平均值方法求出電荷量.
(3)由于cd中無感應電流,則不受安培力,所以cd以gsinθ的加速度下滑,從而下滑的距離表達式可以寫出來,由于△∅=0,所以先表示出初始狀態(tài)的磁通量,再表示出經(jīng)過t后的磁通量,兩者相等,就能寫出B隨時間t的關系式.
解答 解:(1)cd棒勻速運動時速度最大,設為vm,棒中感應電動分為E,電流為I,則
E=BLvm,$I=\frac{E}{2R}$
由平衡條件得:mgsinθ=BIL
代入數(shù)據(jù)解得:vm=1m/s
(2)設cd從開始運動到達最大速度的過程中,經(jīng)過的時間為t,通過的距離為x,cd棒中平均感應電動勢E1,
平均電流為I1,通過cd棒橫截面的電荷量為q,由能守恒定律得:
$mgxsinθ=\frac{1}{2}m{{v}_{m}}^{2}+2Q$,
代入得到x=1m,
所以通過cd棒的電荷量:
$q={I}_{1}t=\frac{{E}_{1}}{2R}t=\frac{\frac{{B}_{2}Lx}{t}}{2R}t=\frac{{B}_{2}Lx}{2R}=\frac{1×1×1}{2×0.5}$=1C
(3)設cd棒開始運動時穿過回路的磁通量為∅0,cd棒在傾斜軌道上下滑的過程中,設加速大小為a,
經(jīng)過時間t通過的距離為x1,穿過回路的磁通量為Φ,cd棒在傾斜軌道上下滑時間為t0,則:
∅0=${B}_{0}L\frac{h}{sinθ}$
加速度:a=gxinθ
位移:${x}_{1}=\frac{1}{2}a{t}^{2}$
而 Φ=$BL(\frac{h}{sinθ}-{x}_{1})$
當cd棒下滑到最低點時有:
$\frac{h}{sinθ}=\frac{1}{2}a{{t}_{0}}^{2}$
解得:${t}_{0}=\sqrt{8}s$
為使cd棒中無感應電流,必須有:∅0=Φ
解得$B=\frac{8}{8-{t}^{2}}$ ($t<\sqrt{8}s$ )
答:(1)導體棒cd沿斜軌道下滑的最大速度的大小為1m/s.
(2)若已知從開始運動到cd棒達到最大速度的過程中,ab棒產(chǎn)生的焦耳熱Q=0.45J,該過程中通過cd棒橫截面的電荷量為1C.
(3)若已知cd棒開始運動時距水平軌道高度h=10m,cd棒由靜止釋放后,為使cd棒中無感應電流,可讓磁場Ⅱ的磁感應強度隨時間變化,將cd棒開始運動的時刻記為t=0,此時磁場Ⅱ的磁感應強度為B0=1T,cd棒在傾斜軌道上下滑的這段時間內(nèi),磁場Ⅱ的磁感應強度B隨時間t變化的關系式為$B=\frac{8}{8-{t}^{2}}$ ($t<\sqrt{8}s$ ).
點評 本題要注意的是:①看起來是雙桿問題,但由于ab受到向下的安培力,則ab始終靜止,實際是單桿問題.②cd下滑又要求無感應電流,則任意時間t回路的磁通量相等,分別表示出初、末狀態(tài)的磁通量,則B隨時間t的關系式就能求出.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中物理 來源: 題型:選擇題
| A. | 1 N | B. | 0.1 N | C. | 10 N | D. | 100 N |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
 某同學對四個電阻各進行了一次測量,把每個電阻兩端的電壓和通過它的電流在U-I坐標系中描點,如圖所示的a、b、c、d所示( )
某同學對四個電阻各進行了一次測量,把每個電阻兩端的電壓和通過它的電流在U-I坐標系中描點,如圖所示的a、b、c、d所示( )| A. | a的電阻大于d的電阻 | B. | b的電阻大于c的電阻 | ||
| C. | c的電阻大于d的電阻 | D. | d的電阻大于a的電阻 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
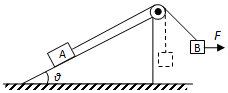 斜面放置于粗糙水平地面上,物塊A通過跨過光滑定滑輪的輕質(zhì)細繩與物塊B連接,一水平力F作用于B上,整個系統(tǒng)處于靜止狀態(tài),如圖所示.現(xiàn)保持F方向不變,使B緩慢地移動到滑輪的正下方,該過程中A與斜面始終保持靜止,在此過程中( )
斜面放置于粗糙水平地面上,物塊A通過跨過光滑定滑輪的輕質(zhì)細繩與物塊B連接,一水平力F作用于B上,整個系統(tǒng)處于靜止狀態(tài),如圖所示.現(xiàn)保持F方向不變,使B緩慢地移動到滑輪的正下方,該過程中A與斜面始終保持靜止,在此過程中( )| A. | 斜面對物塊A的摩擦力一直減小 | B. | 繩對滑輪的作用力保持不變 | ||
| C. | 地面對斜面的摩擦力一直減小 | D. | 地面對斜面的支持力保持不變 |
查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
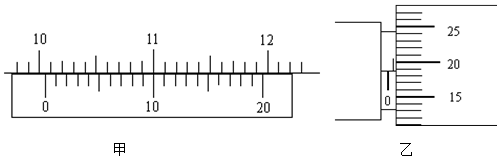
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 庫侖發(fā)現(xiàn)了電流的磁效應 | |
| B. | 麥克斯韋建立了完整的電磁場理論并首先驗證了電磁波存在 | |
| C. | 法拉第發(fā)現(xiàn)了磁場產(chǎn)生電流的條件和規(guī)律 | |
| D. | 伽利略提出的萬有引力定律奠定了天體力學的基礎 |
查看答案和解析>>
科目:高中物理 來源: 題型:計算題
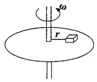 如圖所示,有一臺水平轉(zhuǎn)盤,盤上有一質(zhì)量為m 的物體離轉(zhuǎn)軸的距離為r,中間用一根細線相連,物體和轉(zhuǎn)盤之間的動摩擦因數(shù)為μ,細線所能承受的最大拉力為3μmg,當圓盤靜止時,細線伸直但沒有拉力,求:
如圖所示,有一臺水平轉(zhuǎn)盤,盤上有一質(zhì)量為m 的物體離轉(zhuǎn)軸的距離為r,中間用一根細線相連,物體和轉(zhuǎn)盤之間的動摩擦因數(shù)為μ,細線所能承受的最大拉力為3μmg,當圓盤靜止時,細線伸直但沒有拉力,求:查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
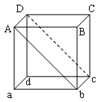 如圖所示,把一邊長為L的勻質(zhì)立方體,繞bc棱翻倒,當AbcD平面處于豎直位置時,它的重心位置升高了( )
如圖所示,把一邊長為L的勻質(zhì)立方體,繞bc棱翻倒,當AbcD平面處于豎直位置時,它的重心位置升高了( )| A. | $\frac{L}{2}$ | B. | $\frac{\sqrt{2}L}{2}$ | C. | $\frac{(2-\sqrt{2})L}{2}$ | D. | 以上答案都不對 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com