
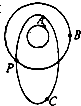
 如圖所示,A為靜止于地球赤道上的物體,B為繞地球做勻速圓周運動軌道半徑為r的衛星,C為繞地球沿橢圓軌道運動的衛星,長軸大小為a,P為B、C兩衛星軌道的交點,已知A、B、C繞地心運動的周期相同,下列說法正確的是( )
如圖所示,A為靜止于地球赤道上的物體,B為繞地球做勻速圓周運動軌道半徑為r的衛星,C為繞地球沿橢圓軌道運動的衛星,長軸大小為a,P為B、C兩衛星軌道的交點,已知A、B、C繞地心運動的周期相同,下列說法正確的是( )| A. | 物體A的線速度大于衛星B的線速度 | |
| B. | 衛星B離地面的高度可以為任意值 | |
| C. | a與r長度關系滿足a=2r | |
| D. | 若已知物體A的周期和萬有引力常量,可求出地球的平均密度 |
分析 抓住A、B的周期相等,根據v=$\frac{2πr}{T}$比較線速度的大小.根據衛星B的周期一定,根據萬有引力提供向心力確定出軌道半徑一定,高度一定.根據開普勒第三定律比較a與r的關系.根據萬有引力提供向心力,結合周期與軌道半徑求出地球的質量,根據密度公式判斷能否求出地球的平均密度.
解答 解:A、因為A、B繞地心運動的周期相同,根據v=$\frac{2πr}{T}$知,B的軌道半徑大于地球的半徑,則物體A的線速度小于衛星B的線速度,故A錯誤.
B、因為B的周期與地球的自轉周期相同,為定值,根據$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$知,r=$\root{3}{\frac{GM{T}_{\;}^{2}}{4{π}_{\;}^{2}}}$,可知軌道半徑恒定,則衛星B離地的高度恒定,不是任意值,故B錯誤.
C、根據開普勒第三定律知,$\frac{{r}_{\;}^{3}}{{T}_{\;}^{2}}=k$,因為周期相等,則橢圓的半長軸與圓軌道半徑相等,即$\frac{a}{2}=r$,故C正確.
D、因為A、B、C繞地心運動的周期相同,若A的周期已知設為T,則B的周期也為T,
對B:根據$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$知,地球的質量M=$\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}$,則地球的平均密度ρ=$\frac{M}{\frac{4π{R}_{\;}^{3}}{3}}$,因為地球的半徑未知,則無法求出地球的密度,故D錯誤.
故選:C.
點評 本題考查了萬有引力定律、開普勒定律與圓周運動的綜合,知道A做圓周運動,不是靠萬有引力提供向心力,抓住A、B的周期相等,結合線速度與周期的關系比較線速度大小.


 黃岡創優卷系列答案
黃岡創優卷系列答案科目:高中物理 來源: 題型:實驗題
 在“研究電磁感應現象”的實驗中,所用的器材如圖所示.
在“研究電磁感應現象”的實驗中,所用的器材如圖所示.查看答案和解析>>
科目:高中物理 來源: 題型:計算題
查看答案和解析>>
科目:高中物理 來源: 題型:實驗題

查看答案和解析>>
科目:高中物理 來源: 題型:計算題
查看答案和解析>>
科目:高中物理 來源: 題型:計算題

查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 半徑一定時,線速度與角速度成正比 | |
| B. | 周期一定時,線速度與角速度成正比 | |
| C. | 線速度一定時,角速度與半徑成正比 | |
| D. | 角速度一定時,線速度與半徑成反比 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 甲比乙先著地 | B. | 甲比乙的加速度大 | ||
| C. | 甲與乙同時著地 | D. | 甲比乙落地速度大 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com