
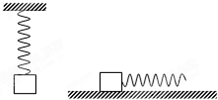
 原長l0=12cm的彈簧,上端固定,下端掛質量為m=4kg的物塊,靜止時彈簧長度l1=20cm.當將該物塊放在水平桌面上,并用上述彈簧沿水平方向拉物塊.當彈簧長度為l2=15cm時,物塊恰好被拉動.此后為保持物塊做勻速直線運動,彈簧長度維持在l3=14cm..求:
原長l0=12cm的彈簧,上端固定,下端掛質量為m=4kg的物塊,靜止時彈簧長度l1=20cm.當將該物塊放在水平桌面上,并用上述彈簧沿水平方向拉物塊.當彈簧長度為l2=15cm時,物塊恰好被拉動.此后為保持物塊做勻速直線運動,彈簧長度維持在l3=14cm..求: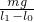 =
=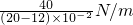 =500N/m
=500N/m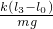 =
=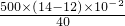 =0.25
=0.25

科目:高中物理 來源: 題型:
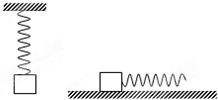 原長l0=12cm的彈簧,上端固定,下端掛質量為m=4kg的物塊,靜止時彈簧長度l1=20cm.當將該物塊放在水平桌面上,并用上述彈簧沿水平方向拉物塊.當彈簧長度為l2=15cm時,物塊恰好被拉動.此后為保持物塊做勻速直線運動,彈簧長度維持在l3=14cm..求:
原長l0=12cm的彈簧,上端固定,下端掛質量為m=4kg的物塊,靜止時彈簧長度l1=20cm.當將該物塊放在水平桌面上,并用上述彈簧沿水平方向拉物塊.當彈簧長度為l2=15cm時,物塊恰好被拉動.此后為保持物塊做勻速直線運動,彈簧長度維持在l3=14cm..求:查看答案和解析>>
科目:高中物理 來源: 題型:
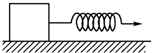 一根彈簧原長l0=10cm,勁度系數為k=200N/m,用此彈簧水平拉一重為20N的物體,如圖所示.
一根彈簧原長l0=10cm,勁度系數為k=200N/m,用此彈簧水平拉一重為20N的物體,如圖所示.查看答案和解析>>
科目:高中物理 來源:0103 期中題 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com