日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

【題目】已知橢圓的焦距為2，過右焦點和短軸一個端點的直線的斜率為，為坐標原點.

（1）求橢圓的方程；

（2）設點，直線與橢圓C交于兩個不同點P，Q，直線AP與x軸交于點M，直線AQ與x軸交于點N，若|OM|·|ON|=2，求證：直線l經過定點.

（Ⅰ）估計該校學生中上個月A，B兩種支付方式都使用的人數；

（Ⅱ）從樣本僅使用B的學生中隨機抽取1人，求該學生上個月支付金額大于2000元的概率；

（Ⅲ）已知上個月樣本學生的支付方式在本月沒有變化．現從樣本僅使用B的學生中隨機抽查1人，發現他本月的支付金額大于2000元．結合（Ⅱ）的結果，能否認為樣本僅使用B的學生中本月支付金額大于2000元的人數有變化？說明理由．

設函數

（Ⅰ）若是函數的極值點，1和是的兩個不同零點，且

且，求的值；

（Ⅱ）若對任意, 都存在（ 為自然對數的底數），使得

成立，求實數的取值范圍.

A地：中位數為2，極差為5； B地：總體平均數為2，眾數為2；

C地：總體平均數為1，總體方差大于0； D地：總體平均數為2，總體方差為3.

則以上四地中，一定符合沒有發生大規模群體感染標志的是_______(填A、B、C、D)

【題目】端午節（每年農歷五月初五），是中國傳統節日，有吃粽子的習俗.某超市在端午節這一天，每售出kg粽子獲利潤元，未售出的粽子每kg虧損元.根據歷史資料，得到銷售情況與市場需求量的頻率分布表，如下表所示.該超市為今年的端午節預購進了kg粽子.以（單位：kg，）表示今年的市場需求量，（單位：元）表示今年的利潤.

（1）將表示為的函數；

（2）在頻率分布表的市場需求量分組中，以各組的區間中間值代表該組的各個值，需求量落入該區間的頻率作為需求量取該區間中間值的概率（例如：若需求量，則取，且的概率等于需求量落入的頻率），求的數學期望.

【題目】已知拋物線，過的直線與拋物線相交于兩點.

（1）若點是點關于坐標原點的對稱點，求面積的最小值；

（2）是否存在垂直于軸的直線，使得被以為直徑的圓截得的弦長恒為定值？若存在，求出的方程和定值；若不存在，說明理由.

【題目】已知函數，.

(1)討論函數的單調性；

(2)若是函數的兩個不同的零點，求證：.

【題目】已知曲線上的點到點的距離比到直線的距離小.

(1)求曲線的方程；

(2)設為曲線上任意一點，點，問是否存在垂直于軸的直線，使得被以為直徑的圓是的弦長恒為定值？若存在，求出的方程和定值；若不存在，說明理由.

【題目】端午節（每年農歷五月初五），是中國傳統節日，有吃粽子的習俗．某超市在端午節這一天，每售出kg粽子獲利潤元，未售出的粽子每kg虧損元．根據歷史資料，得到銷售情況與市場需求量的頻率分布表，如下表所示.該超市為今年的端午節預購進了kg粽子.以（單位：kg，）表示今年的市場需求量，（單位：元）表示今年的利潤．

(1)將表示為的函數；

(2)根據頻率分布表估計今年利潤不少于元的概率．

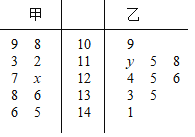
（1）若景點甲中的數據的中位數是125，景點乙中的數據的平均數是124，求x，y的值；

（2）若將圖中景點甲中的數據作為該景點較長一段時期內的樣本數據.今從這段時期中任取4天，記其中游客數超過120人的天數為，求概率；

（3）現從如圖所示的共20天的數據中任取2天的數據（甲、乙兩景點中各取1天），記其中游客數不低于115且不高于125人的天數為，求的分布列和期望.