
科目: 來源: 題型:
【題目】某房地產公司新建小區有A、B兩種戶型住宅,其中A戶型住宅每套面積為100平方米,B戶型住宅每套面積為80平方米,該公司準備從兩種戶型住宅中各拿出12套銷售給內部員工,表是這24套住宅每平方米的銷售價格:(單位:萬元平方米):
房號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
A戶型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.5 |
B戶型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8 | 3.9 | 4.2 | 4.1 | 4.1 | 4.2 | 4.3 | 4.5 |
(1)根據表格數據,完成下列莖葉圖,并分別求出A,B兩類戶型住宅每平方米銷售價格的中位數;
A戶型 | B戶型 | |
2. | ||
3. | ||
4. |
(2)該公司決定對上述24套住房通過抽簽方式銷售,購房者根據自己的需求只能在其中一種戶型中通過抽簽方式隨機獲取房號,每位購房者只有一次抽簽機會,小明是第一位抽簽的員工,經測算其購買能力最多為320萬元,抽簽后所抽得住房價格在其購買能力范圍內則確定購買,否則,將放棄此次購房資格,為了使其購房成功的概率更大,他應該選擇哪一種戶型抽簽?
查看答案和解析>>
科目: 來源: 題型:
【題目】十九世紀末,法國學者貝特朗在研究幾何概型時提出了“貝特朗悖論”,即“在一個圓內任意選一條弦,這條弦的弦長長于這個圓的內接等邊三角形邊長的概率是多少?”貝特朗用“隨機半徑”、“隨機端點”、“隨機中點”三個合理的求解方法,但結果都不相同.該悖論的矛頭直擊概率概念本身,強烈地刺激了概率論基礎的嚴格化.已知“隨機端點”的方法如下:設A為圓O上一個定點,在圓周上隨機取一點B,連接AB,所得弦長AB大于圓O的內接等邊三角形邊長的概率.則由“隨機端點”求法所求得的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】已知動點![]() 到直線
到直線![]() 的距離比到定點
的距離比到定點![]() 的距離大1.
的距離大1.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程.
的方程.
(2)若![]() 為直線
為直線![]() 上一動點,過點
上一動點,過點![]() 作曲線
作曲線![]() 的兩條切線
的兩條切線![]() ,
,![]() ,切點為
,切點為![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.
①求證:![]() 軸;
軸;
②直線![]() 是否恒過一定點?若是,求出這個定點的坐標;若不是,請說明理由.
是否恒過一定點?若是,求出這個定點的坐標;若不是,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】某市政府為減輕汽車尾氣對大氣的污染,保衛藍天,鼓勵廣大市民使用電動交通工具出行,決定為電動車(含電動自行車和電動汽車)免費提供電池檢測服務.現從全市已掛牌照的![]() 電動車中隨機抽取100輛委托專業機構免費為它們進行電池性能檢測,電池性能分為需要更換、尚能使用、較好、良好四個等級,并分成電動自行車和電動汽車兩個群體分別進行統計,樣本分布如圖.
電動車中隨機抽取100輛委托專業機構免費為它們進行電池性能檢測,電池性能分為需要更換、尚能使用、較好、良好四個等級,并分成電動自行車和電動汽車兩個群體分別進行統計,樣本分布如圖.
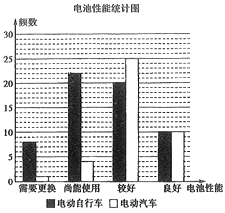
(1)采用分層抽樣的方法從電池性能較好的電動車中隨機抽取9輛,再從這9輛中隨機抽取2輛,求至少有一輛為電動汽車的概率;
(2)為進一步提高市民對電動車的使用熱情,市政府準備為電動車車主一次性發放補助,標準如下:①電動自行車每輛補助300元;②電動汽車每輛補助500元;③對電池需要更換的電動車每輛額外補助400元.試求抽取的100輛電動車執行此方案的預算;并利用樣本估計總體,試估計市政府執行此方案的預算.
查看答案和解析>>
科目: 來源: 題型:
【題目】中國鐵路總公司相關負責人表示,到2018年底,全國鐵路營業里程達到13.1萬公里,其中高鐵營業里程2.9萬公里,超過世界高鐵總里程的三分之二,下圖是2014年到2018年鐵路和高鐵運營里程(單位:萬公里)的折線圖,以下結論不正確的是( )
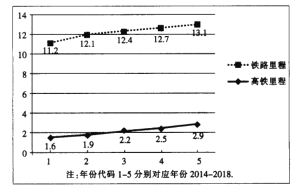
A.每相鄰兩年相比較,2014年到2015年鐵路運營里程增加最顯著
B.從2014年到2018年這5年,高鐵運營里程與年價正相關
C.2018年高鐵運營里程比2014年高鐵運營里程增長80%以上
D.從2014年到2018年這5年,高鐵運營里程數依次成等差數列
查看答案和解析>>
科目: 來源: 題型:
【題目】紅鈴蟲是棉花的主要害蟲之一,能對農作物造成嚴重傷害,每只紅鈴蟲的平均產卵數y和平均溫度x有關,現收集了以往某地的7組數據,得到下面的散點圖及一些統計量的值.(表中![]() )
)
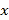
平均溫度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 | ||
平均產卵數 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | ||
|
|
|
|
| |||||
27.429 | 81.286 | 3.612 | 40.182 | 147.714 | |||||
(1)根據散點圖判斷,![]() 與
與![]() (其中
(其中![]() 自然對數的底數)哪一個更適宜作為平均產卵數y關于平均溫度x的回歸方程類型?(給出判斷即可,不必說明理由)并由判斷結果及表中數據,求出y關于x的回歸方程.(計算結果精確到小數點后第三位)
自然對數的底數)哪一個更適宜作為平均產卵數y關于平均溫度x的回歸方程類型?(給出判斷即可,不必說明理由)并由判斷結果及表中數據,求出y關于x的回歸方程.(計算結果精確到小數點后第三位)
(2)根據以往統計,該地每年平均溫度達到28℃以上時紅鈴蟲會造成嚴重傷害,需要人工防治,其他情況均不需要人工防治記該地每年平均溫度達到28℃以上的概率為![]() .
.
①記該地今后5年中,恰好需要3次人工防治的概率為![]() ,求
,求![]() 的最大值,并求出相應的概率p.
的最大值,并求出相應的概率p.
②當![]() 取最大值時,記該地今后5年中,需要人工防治的次數為X,求X的數學期望和方差.
取最大值時,記該地今后5年中,需要人工防治的次數為X,求X的數學期望和方差.
附:線性回歸方程系數公式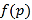 .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】在平面直角坐標系xOy中,橢圓C的中心在坐標原點O,其右焦點為![]() ,且點
,且點![]() 在橢圓C上.
在橢圓C上.
![]() 求橢圓C的方程;
求橢圓C的方程;
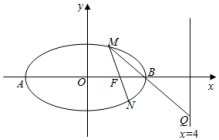
![]() 設橢圓的左、右頂點分別為A、B,M是橢圓上異于A,B的任意一點,直線MF交橢圓C于另一點N,直線MB交直線
設橢圓的左、右頂點分別為A、B,M是橢圓上異于A,B的任意一點,直線MF交橢圓C于另一點N,直線MB交直線![]() 于Q點,求證:A,N,Q三點在同一條直線上.
于Q點,求證:A,N,Q三點在同一條直線上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com