日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

【題目】在平面直角坐標系xOy中，直線l的參數方程為（為參數），在以O為極點，x軸的非負半軸為極軸的極坐標系中，曲線C的極坐標方程為

（1）求曲線C的直角坐標方程

（2）設直線l與x軸交于點P，且與曲線C相交與A、B兩點，若是與的等比中項，求實數m的值

【題目】已知函數，，直線與曲線y=f（x）和y=g（x）分別交于M，N兩點，設曲線y=f（x）在點M處的切線為，在點N處的切線為

（1）當b=1時，若，求a的值

（2）若，求實數a的取值范圍

【題目】已知AOB的一個頂點O是拋物線C：的頂點，A、B兩點都在C上，且=0，

（1）證明：直線AB恒過定點P（2，0）

（2）求AOB面積的最小值

【題目】在四棱錐P-ABCD中，PA平面ABCD，菱形ABCD的邊長為2，且，點E、F分別是PA，CD的中點，

（1）求證：EF平面PBC

（2）若PC與平面ABCD所成角的大小為，求C到平面PBD的距離

（1）若私家車的數量與年份編號滿足線性相關關系，求關于的線性回歸方程，并預測2020年該小區的私家車數量；

（2）小區于2018年底完成了基礎設施改造，劃設了120個停車位．為解決小區車輛亂停亂放的問題，加強小區管理，物業公司決定禁止無車位的車輛進入小區．由于車位有限，物業公司決定在2019年度采用網絡競拍的方式將車位對業主出租，租期一年，競拍方案如下：①截至2018年己登記在冊的私家車業主擁有競拍資格；②每車至多中請一個車位，由車主在競拍網站上提出申請并給出自己的報價；③根據物價部門的規定，競價不得超過1200元；④申請階段截止后，將所有申請的業主報價自高到低排列，排在前120位的業主以其報價成交；⑤若最后出現并列的報價，則以提出申請的時間在前的業主成交，為預測本次競拍的成交最低價，物業公司隨機抽取了有競拍資格的40位業主，進行了競拍意向的調查，并對他們的擬報競價進行了統計，得到如圖頻率分布直方圖：

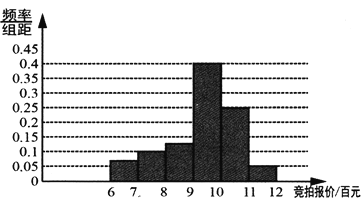
（i）求所抽取的業主中有意向競拍報價不低于1000元的人數；

（ii）如果所有符合條件的車主均參與競拍，利用樣本估計總體的思想，請你據此預測至少需要報價多少元才能競拍車位成功？（精確到整數）

參考公式及數據：對于一組數據，其回歸方程的斜率和截距的最小二乘估計分別為：；．

【題目】在直角坐標系中，直線的參數方程是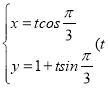為參數），曲線的參數方程是為參數），以為極點，軸的非負半軸為極軸建立極坐標系．

（1）求直線和曲線的極坐標方程；

（2）已知射線與曲線交于兩點，射線與直線交于點，若的面積為1，求的值和弦長．

【題目】已知函數，．

求函數的單調區間和極值；

設，且、是曲線上的任意兩點，若對任意的，直線AB的斜率恒大于常數m，求m的取值范圍．

【題目】三國時代吳國數學家趙爽所注《周髀算經》中給出了勾股定理的絕妙證明.下面是趙爽的弦圖及注文，弦圖是一個以勾股形之弦為邊的正方形，其面積稱為弦實.圖中包含四個全等的勾股形及一個小正方形，分別涂成紅（朱）色及黃色，其面積稱為朱實、黃實，利用，化簡，得.設勾股形中勾股比為，若向弦圖內隨機拋擲顆圖釘（大小忽略不計），則落在黃色圖形內的圖釘數大約為（ ）

A. B. C. D.

【題目】若橢圓的離心率等于，拋物線的焦點在橢圓的頂點上.

（1）求拋物線的方程；

（2）若過的直線與拋物線交于、兩點，又過、作拋物線的切線、,當時，求直線的方程.

【題目】已知曲線的極坐標方程是，曲線的極坐標方程是，正三角形的頂點都在上，且按逆時針次序排列，點的極坐標為，以極點為坐標原點，極軸為軸的正半軸建立平面直角坐標系.

（1）求曲線的直角坐標方程及點的直角坐標；

（2）設為上任意一點，求的取值范圍.