
科目: 來源: 題型:
【題目】如圖所示,某班一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的污損,其中,頻率分布直方圖的分組區(qū)間分別為![]() ,據此解答如下問題.
,據此解答如下問題.
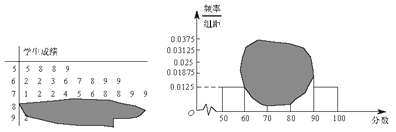
(Ⅰ)求全班人數及分數在![]() 之間的頻率;
之間的頻率;
(Ⅱ)現從分數在![]() 之間的試卷中任取 3 份分析學生情況,設抽取的試卷分數在
之間的試卷中任取 3 份分析學生情況,設抽取的試卷分數在![]() 的份數為
的份數為![]() ,求
,求![]() 的分布列和數學望期.
的分布列和數學望期.
查看答案和解析>>
科目: 來源: 題型:
【題目】某學校為更好進行校紀、校風管理,爭創(chuàng)文明學校,由志愿者組成“小紅帽”監(jiān)督崗,對全校的不文明行為進行監(jiān)督管理,對有不文明行為者進行批評教育,并作詳細的登記,以便跟蹤調查下表是![]() 個周內不文明行為人次統計數據:
個周內不文明行為人次統計數據:
周次 |
|
|
|
|
|
不文明行為人次 |
|
|
|
|
|
(1)請利用所給數據求不文明人次![]() 與周次
與周次![]() 之間的回歸直線方程
之間的回歸直線方程![]() ,并預測該學校第
,并預測該學校第![]() 周的不文明人次;
周的不文明人次;
(2)從第![]() 周到第
周到第![]() 周記錄得知,高一年級有
周記錄得知,高一年級有![]() 位同學,高二年級有
位同學,高二年級有![]() 位同學已經有
位同學已經有![]() 次不文明行為.學校德育處決定先從這
次不文明行為.學校德育處決定先從這![]() 人中任選
人中任選![]() 人進行重點教育,求抽到的兩人恰好來自同一年級的概率
人進行重點教育,求抽到的兩人恰好來自同一年級的概率
參考公式: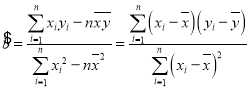 ,
,![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】一片森林原來面積為![]() ,計劃每年砍伐一些樹,且每年砍伐面積的百分比相等,當砍伐到面積的一半時,所用時間是10年,為保護生態(tài)環(huán)境,森林面積至少要保留原面積的
,計劃每年砍伐一些樹,且每年砍伐面積的百分比相等,當砍伐到面積的一半時,所用時間是10年,為保護生態(tài)環(huán)境,森林面積至少要保留原面積的![]() ,已知到今年為止,森林剩余面積為原來的
,已知到今年為止,森林剩余面積為原來的![]() .
.
(1)到今年為止,該森林已砍伐了多少年?
(2)今后最多還能砍伐多少年?
查看答案和解析>>
科目: 來源: 題型:
【題目】在極坐標系中,射線![]() 與圓
與圓![]() 交于點
交于點![]() ,橢圓
,橢圓![]() 的方程為
的方程為![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸正半軸建立平面直角坐標系
軸正半軸建立平面直角坐標系![]()
(1)求點![]() 的直角坐標和橢圓
的直角坐標和橢圓![]() 的參數方程;
的參數方程;
(2)若![]() 為橢圓
為橢圓![]() 的下頂點,
的下頂點,![]() 為橢圓
為橢圓![]() 上任意一點,求
上任意一點,求![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目: 來源: 題型:
【題目】已知函數![]() ,給出下列結論:
,給出下列結論:
(1)若對任意![]() ,且
,且![]() ,都有
,都有![]() ,則
,則![]() 為R上的減函數;
為R上的減函數;
(2)若![]() 為R上的偶函數,且在
為R上的偶函數,且在![]() 內是減函數,
內是減函數, ![]() (-2)=0,則
(-2)=0,則![]() >0解集為(-2,2);
>0解集為(-2,2);
(3)若![]() 為R上的奇函數,則
為R上的奇函數,則![]() 也是R上的奇函數;
也是R上的奇函數;
(4)t為常數,若對任意的![]() ,都有
,都有![]() 則
則![]() 關于
關于![]() 對稱。
對稱。
其中所有正確的結論序號為_________
查看答案和解析>>
科目: 來源: 題型:
【題目】某大學棋藝協會定期舉辦“以棋會友”的競賽活動,分別包括“中國象棋”、“圍棋”、“五子棋”、“國際象棋”四種比賽,每位協會會員必須參加其中的兩種棋類比賽,且各隊員之間參加比賽相互獨立;已知甲同學必選“中國象棋”,不選“國際象棋”,乙同學從四種比賽中任選兩種參與.
(1)求甲參加圍棋比賽的概率;
(2)求甲、乙兩人參與的兩種比賽都不同的概率.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,上、下頂點分別為
,上、下頂點分別為![]() ,若
,若![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點在橢圓
的對稱點在橢圓![]() 上.
上.
(1)求橢圓![]() 的方程與離心率;
的方程與離心率;
(2)過點![]() 做直線
做直線![]() 與橢圓
與橢圓![]() 相交于兩個不同的點
相交于兩個不同的點![]() ;若
;若![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】在平面直角坐標系![]() 中曲線
中曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以
為參數),以![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,直線
軸的正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程以及直線
的普通方程以及直線![]() 的直角坐標方程;
的直角坐標方程;
(2)將曲線![]() 向左平移2個單位,再將曲線
向左平移2個單位,再將曲線![]() 上的所有點的橫坐標縮短為原來的
上的所有點的橫坐標縮短為原來的![]() ,得到曲線
,得到曲線![]() ,求曲線
,求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
科目: 來源: 題型:
【題目】楊輝,字謙光,南宋時期杭州人.在他1261年所著的《詳解九章算法》一書中,輯錄了如圖所示的三角形數表,稱之為“開方作法本源”圖,并說明此表引自11世紀中葉(約公元1050年)賈憲的《釋鎖算術》,并繪畫了“古法七乘方圖”.故此,楊輝三角又被稱為“賈憲三角”.楊輝三角是一個由數字排列成的三角形數表,一般形式如下:
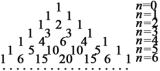
基于上述規(guī)律,可以推測,當![]() 時,從左往右第22個數為_____________.
時,從左往右第22個數為_____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com