
科目: 來源: 題型:
【題目】如圖,關于正方體![]() ,有下列四個命題:
,有下列四個命題:
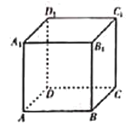
①![]() 與平面
與平面![]() 所成角為45°;
所成角為45°;
②三棱錐![]() 與三棱錐
與三棱錐![]() 的體積比為
的體積比為![]() ;
;
③存在唯一平面![]() .使
.使![]() 平面
平面![]() 且
且![]() 截此正方體所得截面為正六邊形;
截此正方體所得截面為正六邊形;
④過![]() 作平面
作平面![]() ,使得棱
,使得棱![]() 、
、![]() ,
,![]() 在平面
在平面![]() 上的正投影的長度相等.則這樣的平面
上的正投影的長度相等.則這樣的平面![]() 有且僅有一個.
有且僅有一個.
上述四個命題中,正確命題的序號為________.
查看答案和解析>>
科目: 來源: 題型:
【題目】造紙術是我國古代四大發明之一,紙張的規格是指紙張制成后,經過修整切邊,裁成一定的尺寸.現在我國采用國際標準,規定以![]() 、
、![]() 、…、
、…、![]() ;
;![]() 、
、![]() 、…、
、…、![]() 等標記來表示紙張的幅面規格.復印紙幅面規格只采用
等標記來表示紙張的幅面規格.復印紙幅面規格只采用![]() 系列和
系列和![]() 系列,共中
系列,共中![]() 系列的幅面規格為:①
系列的幅面規格為:①![]() 規格的紙張的幅寬(以
規格的紙張的幅寬(以![]() 表示)和長度(以
表示)和長度(以![]() 表示)的比例關系為
表示)的比例關系為![]() ;②將
;②將![]() 紙張沿長度方向對開成兩等分,便成為
紙張沿長度方向對開成兩等分,便成為![]() 規格,
規格,![]() 紙張沿長度方向對開成兩等分,便成為
紙張沿長度方向對開成兩等分,便成為![]() 規格,…,如此對開至
規格,…,如此對開至![]() 規格.現有
規格.現有![]() 、
、![]() 、
、![]() 、…、
、…、![]() 紙各一張.若
紙各一張.若![]() 紙的面積為
紙的面積為![]() .則這9張紙的面積之和等于__________
.則這9張紙的面積之和等于__________![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】天文學中為了衡量星星的明暗程度,古希臘天文學家喜帕恰斯(![]() ,又名依巴谷)在公元前二世紀首先提出了星等這個概念.星等的數值越小,星星就越亮;星等的數值越大,它的光就越暗.到了1850年,由于光度計在天體光度測量中的應用,英國天文學家普森(
,又名依巴谷)在公元前二世紀首先提出了星等這個概念.星等的數值越小,星星就越亮;星等的數值越大,它的光就越暗.到了1850年,由于光度計在天體光度測量中的應用,英國天文學家普森(![]() )又提出了衡量天體明暗程度的亮度的概念.天體的明暗程度可以用星等或亮度來描述.兩顆星的星等與亮度滿足
)又提出了衡量天體明暗程度的亮度的概念.天體的明暗程度可以用星等或亮度來描述.兩顆星的星等與亮度滿足![]() .其中星等為
.其中星等為![]() 的星的亮度為
的星的亮度為![]() .已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的
.已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的![]() 倍,則與
倍,則與![]() 最接近的是(當
最接近的是(當![]() 較小時,
較小時, ![]() )
)
A.1.24B.1.25C.1.26D.1.27
查看答案和解析>>
科目: 來源: 題型:
【題目】在平面直角坐標系![]() 中,過點
中,過點![]() 的動圓恒與
的動圓恒與![]() 軸相切,
軸相切,![]() 為該圓的直徑,設點
為該圓的直徑,設點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 的任意直線
的任意直線![]() 與曲線
與曲線![]() 交于點
交于點![]() ,
,![]() 為
為![]() 的中點,過點
的中點,過點![]() 作
作![]() 軸的平行線交曲線
軸的平行線交曲線![]() 于點
于點![]() ,
,![]() 關于點
關于點![]() 的對稱點為
的對稱點為![]() ,除
,除![]() 以外,直線
以外,直線![]() 與
與![]() 是否有其它公共點?說明理由.
是否有其它公共點?說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】某公司為了對某種商品進行合理定價,需了解該商品的月銷售量![]() (單位:萬件)與月銷售單價
(單位:萬件)與月銷售單價![]() (單位:元/件)之間的關系,對近
(單位:元/件)之間的關系,對近![]() 個月的月銷售量
個月的月銷售量![]() 和月銷售單價
和月銷售單價![]()
![]() 數據進行了統計分析,得到一組檢測數據如表所示:
數據進行了統計分析,得到一組檢測數據如表所示:
月銷售單價 |
|
|
|
|
|
|
月銷售量 |
|
|
|
|
|
|
(1)若用線性回歸模型擬合![]() 與
與![]() 之間的關系,現有甲、乙、丙三位實習員工求得回歸直線方程分別為:
之間的關系,現有甲、乙、丙三位實習員工求得回歸直線方程分別為:![]() ,
,![]() 和
和![]() ,其中有且僅有一位實習員工的計算結果是正確的.請結合統計學的相關知識,判斷哪位實習員工的計算結果是正確的,并說明理由;
,其中有且僅有一位實習員工的計算結果是正確的.請結合統計學的相關知識,判斷哪位實習員工的計算結果是正確的,并說明理由;
(2)若用![]() 模型擬合
模型擬合![]() 與
與![]() 之間的關系,可得回歸方程為
之間的關系,可得回歸方程為![]() ,經計算該模型和(1)中正確的線性回歸模型的相關指數
,經計算該模型和(1)中正確的線性回歸模型的相關指數![]() 分別為
分別為![]() 和
和![]() ,請用
,請用![]() 說明哪個回歸模型的擬合效果更好;
說明哪個回歸模型的擬合效果更好;
(3)已知該商品的月銷售額為![]() (單位:萬元),利用(2)中的結果回答問題:當月銷售單價為何值時,商品的月銷售額預報值最大?(精確到
(單位:萬元),利用(2)中的結果回答問題:當月銷售單價為何值時,商品的月銷售額預報值最大?(精確到![]() )
)
參考數據:![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為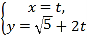 (
(![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)已知點![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于點
相交于點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 來源: 題型:
【題目】為提高產品質量,某企業質量管理部門經常不定期地抽查產品進行檢測,現在某條生產線上隨機抽取100個產品進行相關數據的對比,并對每個產品進行綜合評分(滿分100分),將每個產品所得的綜合評分制成如圖所示的頻率分布直方圖.記綜合評分為80分及以上的產品為一等品.
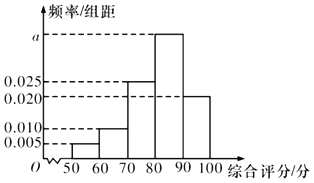
(1)求圖中![]() 的值,并求綜合評分的中位數;
的值,并求綜合評分的中位數;
(2)用樣本估計總體,以頻率作為概率,按分層抽樣的思想,先在該條生產線中隨機抽取5個產品,再從這5個產品中隨機抽取2個產品記錄有關數據,求這2個產品中恰有一個一等品的概率.
查看答案和解析>>
科目: 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).在以坐標原點為極點,
為參數).在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 相交于
相交于![]()
![]() 兩點,求
兩點,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com