
科目: 來源: 題型:
【題目】某廠有4臺大型機器,在一個月中,一臺機器至多出現1次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需1名工人進行維修,每臺機器出現故障需要維修的概率為![]() .
.
(1)問該廠至少有多少名維修工人才能保證每臺機器在任何時刻同時出現故障時能及時進行維修的概率不小于![]() ?
?
(2)已知1名工人每月只有維修1臺機器的能力,每月需支付給每位工人1萬元的工資,每臺機器不出現故障或出現故障能及時維修,能使該廠產生5萬元的利潤,否則將不產生利潤.若該廠現有2名工人,求該廠每月獲利的均值.
查看答案和解析>>
科目: 來源: 題型:
【題目】某中學將100名高一新生分成水平相同的甲,乙兩個“平行班”,每班50人.陳老師采用A,B兩種不同的教學方式分別在甲,乙兩個班級進行教改實驗.為了解教學效果,期末考試后,陳老師分別從兩個班級中各隨機抽取20名學生的成績進行統計,作出莖葉圖如下,計成績不低于90分者為“成績優秀”.

(1)從乙班樣本的20個個體中,從不低于86分的成績中隨機抽取2個,求抽出的兩個均“成績優秀”的概率;
(2)由以上統計數據填寫下面2x2列聯表,并判斷是否有![]() 的把握認為“成績優秀”與教學方式有關.
的把握認為“成績優秀”與教學方式有關.
甲班(A方式) | 乙班(B方式) | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
附: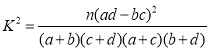
P( | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | /tr>
查看答案和解析>>
科目: 來源: 題型:
【題目】在平面直角坐標系xOy中,已知曲線C1:![]() , 曲線C2:
, 曲線C2:![]() ,以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系. 并在兩種坐標系中取相同的單位長度。
,以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系. 并在兩種坐標系中取相同的單位長度。
(1)寫出曲線C1,C2的極坐標方程;
(2)在極坐標系中,已知點A是射線l:![]() 與C1的交點,點B是l與C2的異于極點的交點,當
與C1的交點,點B是l與C2的異于極點的交點,當![]() 在區間
在區間![]() 上變化時,求
上變化時,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 來源: 題型:
【題目】(本小題滿分13分)
如圖,已知拋物線![]() ,過點
,過點![]() 任作一直線與
任作一直線與![]() 相交于
相交于![]() 兩點,過點
兩點,過點![]() 作
作![]() 軸的平行線與直線
軸的平行線與直線![]() 相交于點
相交于點![]() (
(![]() 為坐標原點).
為坐標原點).

(1)證明:動點![]() 在定直線上;
在定直線上;
(2)作![]() 的任意一條切線
的任意一條切線![]() (不含
(不含![]() 軸)與直線
軸)與直線![]() 相交于點
相交于點![]() ,與(1)中的定直線相交于點
,與(1)中的定直線相交于點![]() ,證明:
,證明:![]() 為定值,并求此定值.
為定值,并求此定值.
查看答案和解析>>
科目: 來源: 題型:
【題目】某地區高考實行新方案,規定:語文、數學和英語是考生的必考科目,考生還須從物理、化學、生物、歷史、地理和政治六個科目中選取三個科目作為選考科目.若一個學生從六個科目中選出了三個科目作為選考科目,則稱該學生的選考方案確定;否則,稱該學生的選考方案待確定.例如,學生甲選擇“物理、化學和生物”三個選考科目,則學生甲的選考方案確定,“物理、化學和生物”為其選考方案.
某學校為了解高一年級![]() 名學生選考科目的意向,隨機選取
名學生選考科目的意向,隨機選取![]() 名學生進行了一次調查,統計選考科目人數如下表:
名學生進行了一次調查,統計選考科目人數如下表:
性別 | 選考方案確定情況 | 物理 | 化學 | 生物 | 歷史 | 地理 | 政治 |
男生 | 選考方案確定的有 |
|
|
|
|
|
|
選考方案待確定的有 |
|
|
|
|
|
| |
女生 | 選考方案確定的有 |
|
|
|
|
|
|
選考方案待確定的有 |
|
|
|
|
|
|
(1)估計該學校高一年級選考方案確定的學生中選考生物的學生有多少人?
(2)假設男生、女生選擇選考科目是相互獨立的.從選考方案確定的![]() 名學生中隨機選出
名學生中隨機選出![]() 名,試求在選取的
名,試求在選取的![]() 名學生中恰有
名學生中恰有![]() 名男生的條件下兩名學生的選考方案中都含有歷史學科的概率;
名男生的條件下兩名學生的選考方案中都含有歷史學科的概率;
(3)從選考方案確定的![]() 名男生中隨機選出
名男生中隨機選出![]() 名,設隨機變量
名,設隨機變量![]() 表示所選
表示所選![]() 人中選考方案完全相同的人數(若有
人中選考方案完全相同的人數(若有![]() 組
組![]() 人選考方案完全相同,則
人選考方案完全相同,則![]() ),求
),求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知動點![]() 到定直線
到定直線![]() :
:![]() 的距離比到定點
的距離比到定點![]() 的距離大2.
的距離大2.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)在![]() 軸正半軸上,是否存在某個確定的點
軸正半軸上,是否存在某個確定的點![]() ,過該點的動直線
,過該點的動直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,使得
兩點,使得![]() 為定值.如果存在,求出點
為定值.如果存在,求出點![]() 坐標;如果不存在,請說明理由.
坐標;如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com