【題目】如圖，在五面體
中，四邊形
為矩形，
為等邊三角形，且平面
平面
.
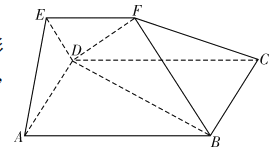
（1）證明：平面平面；
（2）若
，求直線
與平面
所成角的正弦值.
【答案】（1）見解析（2）
【解析】
取
中點
，則
,從而
平面
,進而可得
平面
,由面面垂直的判定即可得證;
取
中點
，以為坐標原點，
為
軸建系.利用空間向量法,求出直線
的方向向量
和平面
的法向量
,求出向量和夾角的余弦值即可.
證明：取中點，因為
為等邊三角形,所以，
又平面
平面，且平面
平面
，
所以平面，則
，
又
，所以平面，
又
平面
，所以平面平面.
取中點，由知平面
平面，
所以
平面，
如圖.以為坐標原點，為軸建系.設
長度為
，
則點坐標為：
，
因為
，所以
平面，
又平面
平面
，
平面
由線面平行的性質知,
，
由共線向量定理知,存在唯一實數
使
，
因為
,所以點
.
則
，
由于
，所以
，
解得
.于是
，
設平面
的法向量為
,
因為
,
所以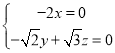
,解得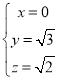
，
從而平面的法向量為
又直線的方向向量為
，
記直線與平面所成角為
，
所以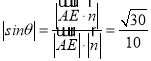
所以直線與平面所成角的正弦值為
科目：高中數學 來源： 題型：
【題目】已知橢圓C：
（a＞b＞0）的兩個焦點分別為F1，F2，離心率為
，過F1的直線l與橢圓C交于M，N兩點，且△MNF2的周長為8．
（1）求橢圓C的方程；
（2）若直線y＝kx＋b與橢圓C分別交于A，B兩點，且OA⊥OB，試問點O到直線AB的距離是否為定值，證明你的結論．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】近幾年一種新奇水果深受廣大消費者的喜愛，一位農戶發揮聰明才智，把這種露天種植的新奇水果搬到了大棚里，收到了很好的經濟效益．根據資料顯示，產出的新奇水果的箱數x（單位：十箱）與成本y（單位：千元）的關系如下：
x | 1 | 3 | 4 | 6 | 7 |
y | 5 | 6．5 | 7 | 7．5 | 8 |
y與x可用回歸方程
（ 其中
，
為常數）進行模擬．
（Ⅰ）若該農戶產出的該新奇水果的價格為150元/箱，試預測該新奇水果100箱的利潤是多少元．|．
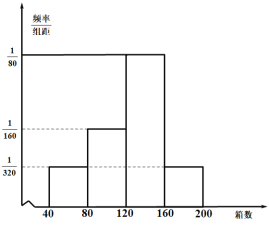
（Ⅱ）據統計，10月份的連續16天中該農戶每天為甲地配送的該新奇水果的箱數的頻率分布直方圖如圖所示．
（i）若從箱數在
內的天數中隨機抽取2天，估計恰有1天的水果箱數在
內的概率；
（ⅱ）求這16天該農戶每天為甲地配送的該新奇水果的箱數的平均值．（每組用該組區間的中點值作代表）
參考數據與公式：設
，則
|
|
|
|
0.54 | 6.8 | 1.53 | 0.45 |
線性回歸直線中，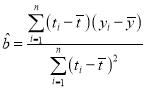
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學將100名高一新生分成水平相同的甲，乙兩個“平行班”，每班50人.陳老師采用A,B兩種不同的教學方式分別在甲，乙兩個班級進行教改實驗.為了解教學效果，期末考試后，陳老師分別從兩個班級中各隨機抽取20名學生的成績進行統計，作出莖葉圖如下，計成績不低于90分者為“成績優秀”.
（1）從乙班樣本的20個個體中，從不低于86分的成績中隨機抽取2個，求抽出的兩個均“成績優秀”的概率；
（2）由以上統計數據填寫下面2x2列聯表，并判斷是否有
的把握認為“成績優秀”與教學方式有關.
甲班（A方式） | 乙班（B方式） | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
附：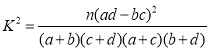
P（ | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | /tr>
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如果無窮數列{an}的所有項恰好構成全體正整數的一個排列，則稱數列{an}具有性質P．
（Ⅰ）若an
（k∈N*），判斷數列{an}是否具有性質P，并說明理由，
（Ⅱ）若數列{an}具有性質P，求證：{an}中一定存在三項ai，aj，ak（i＜j＜k）構成公差為奇數的等差數列；
（Ⅲ）若數列{an}具有性質P，則{an}中是否一定存在四項ai，aj，ak，al，（i＜j＜k＜l）構成公差為奇數的等差數列？證明你的結論．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
