
【題目】已知函數![]() ,其中
,其中![]() ,
,![]() 為自然對數的底數.
為自然對數的底數.
(1)當![]() 時,證明:對
時,證明:對![]() ;
;
(2)若函數![]() 在
在![]() 上存在極值,求實數
上存在極值,求實數![]() 的取值范圍。
的取值范圍。
【答案】(1)見證明;(2) ![]()
【解析】
(1)利用導數說明函數的單調性,進而求得函數的最小值,得到要證明的結論;
(2)問題轉化為導函數在區間上有解,法一:對a分類討論,分別研究a的不同取值下,導函數的單調性及值域,從而得到結論.法二:構造函數,利用函數的導數判斷函數的單調性求得函數的值域,再利用零點存在定理說明函數存在極值.
(1)當![]() 時,
時,![]() ,于是,
,于是,![]() .
.
又因為,當![]() 時,
時,![]() 且
且![]() .
.
故當![]() 時,
時,![]() ,即
,即![]() .
.
所以,函數![]() 為
為![]() 上的增函數,于是,
上的增函數,于是,![]() .
.
因此,對![]() ,
,![]() ;
;
(2) 方法一:由題意![]() 在
在![]() 上存在極值,則
上存在極值,則![]() 在
在![]() 上存在零點,
上存在零點,
①當![]() 時,
時,![]() 為
為![]() 上的增函數,
上的增函數,
注意到![]() ,
,![]() ,
,
所以,存在唯一實數![]() ,使得
,使得![]() 成立.
成立.
于是,當![]() 時,
時,![]() ,
,![]() 為
為![]() 上的減函數;
上的減函數;
當![]() 時,
時,![]() ,
,![]() 為
為![]() 上的增函數;
上的增函數;
所以![]() 為函數
為函數![]() 的極小值點;
的極小值點;
②當![]() 時,
時,![]() 在
在![]() 上成立,
上成立,
所以![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() 在
在![]() 上沒有極值;
上沒有極值;
③當![]() 時,
時,![]() 在
在![]() 上成立,
上成立,
所以![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() 在
在![]() 上沒有極值,
上沒有極值,
綜上所述,使![]() 在
在![]() 上存在極值的
上存在極值的![]() 的取值范圍是
的取值范圍是![]() .
.
方法二:由題意,函數![]() 在
在![]() 上存在極值,則
上存在極值,則![]() 在
在![]() 上存在零點.
上存在零點.
即![]() 在
在![]() 上存在零點.
上存在零點.
設![]() ,
,![]() ,則由單調性的性質可得
,則由單調性的性質可得![]() 為
為![]() 上的減函數.
上的減函數.
即![]() 的值域為
的值域為![]() ,所以,當實數
,所以,當實數![]() 時,
時,![]() 在
在![]() 上存在零點.
上存在零點.
下面證明,當![]() 時,函數
時,函數![]() 在
在![]() 上存在極值.
上存在極值.
事實上,當![]() 時,
時,![]() 為
為![]() 上的增函數,
上的增函數,
注意到![]() ,
,![]() ,所以,存在唯一實數
,所以,存在唯一實數![]() ,
,
使得![]() 成立.于是,當
成立.于是,當![]() 時,
時,![]() ,
,![]() 為
為![]() 上的減函數;
上的減函數;
當![]() 時,
時,![]() ,
,![]() 為
為![]() 上的增函數;
上的增函數;
即![]() 為函數
為函數![]() 的極小值點.
的極小值點.
綜上所述,當![]() 時,函數
時,函數![]() 在
在![]() 上存在極值.
上存在極值.


 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源: 題型:
【題目】等差數列![]() 首項和公差都是
首項和公差都是![]() ,記
,記![]() 的前n項和為
的前n項和為![]() ,等比數列
,等比數列![]() 各項均為正數,公比為q,記
各項均為正數,公比為q,記![]() 的前n項和為
的前n項和為![]() :
:
(1)寫出![]()
![]() 構成的集合A;
構成的集合A;
(2)若將![]() 中的整數項按從小到大的順序構成數列
中的整數項按從小到大的順序構成數列![]() ,求
,求![]() 的一個通項公式;
的一個通項公式;
(3)若q為正整數,問是否存在大于1的正整數k,使得![]()
![]() 同時為(1)中集合A的元素?若存在,寫出所有符合條件的
同時為(1)中集合A的元素?若存在,寫出所有符合條件的![]() 的通項公式,若不存在,請說明理由.
的通項公式,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數學中,布勞威爾不動點定理是拓撲學里一個非常重要的不動點定理,它可應用到有限維空間,并構成一般不動點定理的基石.布勞威爾不動點定理得名于荷蘭數學家魯伊茲·布勞威爾(L.E. J. Brouwer),簡單的講就是對于滿足一定條件的連續函數![]() ,存在一個點
,存在一個點![]() ,使得
,使得![]() ,那么我們稱該函數為“不動點”函數,下列為“不動點”函數的是( )
,那么我們稱該函數為“不動點”函數,下列為“不動點”函數的是( )
A.![]() B.
B.![]()
C.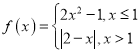 D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠在2016年的“減員增效”中對部分人員實行分流,規定分流人員第一年可以到原單位領取工資的100%,從第二年起,以后每年只能在原單位按上一年的![]() 領取工資,該廠根據分流人員的技術特長,計劃創辦新的經濟實體,該經濟實體預計第一年屬投資階段,第二年每人可獲得
領取工資,該廠根據分流人員的技術特長,計劃創辦新的經濟實體,該經濟實體預計第一年屬投資階段,第二年每人可獲得![]() 元收入,從第三年起每人每年的收入可在上一年的基礎上遞增50%,如果某人分流后工資的收入每年
元收入,從第三年起每人每年的收入可在上一年的基礎上遞增50%,如果某人分流后工資的收入每年![]() 元,分流后進入新經濟實體,第
元,分流后進入新經濟實體,第![]() 年的收入為
年的收入為![]() 元;
元;
(1)求![]() 的通項公式;
的通項公式;
(2)當![]() 時,是否一定可以保證這個人分流一年后的收入永遠超過分流前的年收入?
時,是否一定可以保證這個人分流一年后的收入永遠超過分流前的年收入?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國武漢于2019年10月18日至2019年10月27日成功舉辦了第七屆世界軍人運動會.來自109個國家的9300余名運動員同臺競技.經過激烈的角逐,獎牌榜的前3名如下:
國家 | 金牌 | 銀牌 | 銅牌 | 獎牌總數 |
中國 | 133 | 64 | 42 | 239 |
俄羅斯 | 51 | 53 | 57 | 161 |
巴西 | 21 | 31 | 36 | 88 |
某數學愛好者采用分層抽樣的方式,從中國和巴西獲得金牌選手中抽取了22名獲獎代表.從這22名中隨機抽取3人, 則這3人中中國選手恰好1人的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年北京市百項疏堵工程基本完成.有關部門為了解疏堵工程完成前后早高峰時段公交車運行情況,調取某路公交車早高峰時段全程所用時間(單位:分鐘)的數據,從疏堵工程完成前的數據中隨機抽取5個數據,記為A組,從疏堵工程完成后的數據中隨機抽取5個數據,記為B組.
A組:128,100,151,125,120
B組:100,102,96,101,![]()
己知B組數據的中位數為100,且從中隨機抽取一個數不小于100的概率是![]() .
.
(1)求a的值;
(2)該路公交車全程所用時間不超過100分鐘,稱為“正點運行”從A,B兩組數據中各隨機抽取一個數據,記兩次運行中正點運行的次數為X,求X的分布列及期望;
(3)試比較A,B兩組數據方差的大小(不要求計算),并說明其實際意義.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com