日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

【題目】在平面直角坐標系中，已知橢圓的焦距為4，且過點．

（1）求橢圓的方程

（2）設橢圓的上頂點為，右焦點為，直線與橢圓交于、兩點，問是否存在直線，使得為的垂心，若存在，求出直線的方程；若不存在，說明理由．

【題目】（本小題滿分12分）已知點為拋物線的焦點，點在拋物線上，且．

（Ⅰ）求拋物線的方程；

（Ⅱ）已知點，延長交拋物線于點，證明：以點為圓心且與直線相切的圓，必與直線相切．

【題目】在平面直角坐標系中，直線的參數方程為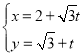（為參數）.在以坐標原點為極點，軸的正半軸為極軸的極坐標系中，曲線C的極坐標方程為.

（1）求直線的極坐標方程及曲線C的直角坐標方程；

（2）若是直線上的一點，是曲線C上的一點，求的最大值.

【題目】在平面直角坐標系中，點，分別為橢圓C：的左右焦點，橢圓的離心率為，點在橢圓C上，不在軸上的動點P與動點Q關于原點O對稱，且四邊形的周長為.

（1）求動點P的軌跡方程；

（2）在動點P的軌跡上有兩個不同的點M，N，線段MN的中點為G，已知點在圓上，求的最大值，并判斷此時ΔOMN的形狀.

（1）根據上面的列聯表判斷，能否在犯錯誤的概率不超過0.001的前提下認為是否贊同小升初錄取辦法與近三年是否家里有小升初學生有關；

（2）從上述調查的不贊同小升初錄取辦法人員中根據近三年家里是否有小升初學生按分層抽樣抽出6人，再從這6人中隨機抽出3人進行電話回訪，求3人中恰有1人近三年家里沒有小升初學生的概率.

附：，其中.

【題目】如圖所示，四邊形ABCD與BDEF均為菱形，，且．

求證：平面BDEF；

求直線AD與平面ABF所成角的正弦值．

【題目】己知函數.(是常數，且（)

（Ⅰ）求函數的單調區間；

（Ⅱ）當在處取得極值時，若關于的方程在上恰有兩個不相等的實數根，求實數的取值范圍；

（Ⅲ）求證:當時.

【題目】已知圓的圓心為，直線l過點且與x軸不重合，l交圓于C，D兩點，過作的平行線，交于點E.設點E的軌跡為.

（1）求的方程；

（2）直線與相切于點M，與兩坐標軸的交點為A與B，直線經過點M且與垂直，與的另一個交點為N，當取得最小值時，求的面積.

A.B.C.D.

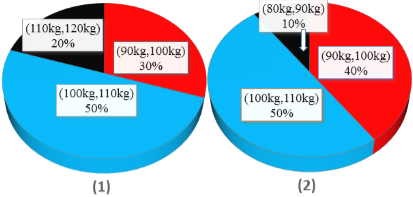
A.他們健身后，體重在區間內的人增加了2個

B.他們健身后，體重在區間內的人數沒有改變

C.他們健身后，20人的平均體重大約減少了8 kg

D.他們健身后，原來體重在區間內的肥胖者體重都有減少