
【題目】在平面直角坐標(biāo)系中,點(diǎn)![]() ,
,![]() 分別為橢圓C:
分別為橢圓C:![]() 的左右焦點(diǎn),橢圓
的左右焦點(diǎn),橢圓![]() 的離心率為
的離心率為![]() ,點(diǎn)
,點(diǎn)![]() 在橢圓C上,不在
在橢圓C上,不在![]() 軸上的動(dòng)點(diǎn)P與動(dòng)點(diǎn)Q關(guān)于原點(diǎn)O對稱,且四邊形
軸上的動(dòng)點(diǎn)P與動(dòng)點(diǎn)Q關(guān)于原點(diǎn)O對稱,且四邊形![]() 的周長為
的周長為![]() .
.
(1)求動(dòng)點(diǎn)P的軌跡方程;
(2)在動(dòng)點(diǎn)P的軌跡上有兩個(gè)不同的點(diǎn)M![]() ,N
,N![]() ,線段MN的中點(diǎn)為G,已知點(diǎn)
,線段MN的中點(diǎn)為G,已知點(diǎn)![]() 在圓
在圓![]() 上,求
上,求![]() 的最大值,并判斷此時(shí)ΔOMN的形狀.
的最大值,并判斷此時(shí)ΔOMN的形狀.
【答案】(1)![]() ;(2)最大值為
;(2)最大值為![]() ,ΔOMN是直角三角形
,ΔOMN是直角三角形
【解析】
(1)題中先求得![]() 的坐標(biāo),即
的坐標(biāo),即![]() ,可利用離心率
,可利用離心率![]() 和點(diǎn)
和點(diǎn)![]() 在橢圓上
在橢圓上 ![]() 結(jié)合
結(jié)合![]() 解得
解得![]()
![]() ,動(dòng)點(diǎn)P與動(dòng)點(diǎn)Q關(guān)于原點(diǎn)O對稱,且四邊形
,動(dòng)點(diǎn)P與動(dòng)點(diǎn)Q關(guān)于原點(diǎn)O對稱,且四邊形![]() 的周長為
的周長為![]() .可得
.可得![]() 點(diǎn)軌跡是橢圓,且長軸長已知,焦距已知,只要再求得短半軸長
點(diǎn)軌跡是橢圓,且長軸長已知,焦距已知,只要再求得短半軸長![]() 即得,注意方程中
即得,注意方程中![]() ;
;
(2)由![]() 用點(diǎn)
用點(diǎn)![]() 都在橢圓上可求得
都在橢圓上可求得![]() ,用兩點(diǎn)間距離公式表示出
,用兩點(diǎn)間距離公式表示出![]() ,代入
,代入![]() 和
和![]() ,并利用基本不等式可求得最大值.根據(jù)取得最大值時(shí)的條件得
,并利用基本不等式可求得最大值.根據(jù)取得最大值時(shí)的條件得![]() 是直角三角形.
是直角三角形.
(1)設(shè)點(diǎn)![]() ,
,![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() ,
,![]()
![]()
由已知可知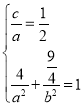 ,又
,又![]() ,所以可得
,所以可得![]() ,則
,則![]() ,
,![]()
連接PQ,因?yàn)?/span>![]() ,OP=OQ,所以四邊形
,OP=OQ,所以四邊形![]() 為平行四邊形.
為平行四邊形.
因?yàn)樗倪呅?/span>![]() 的周長為
的周長為![]() ,所以
,所以![]() ,
,
所以動(dòng)點(diǎn)P的軌跡是以點(diǎn)![]() ,
,![]() 分別為左、右焦點(diǎn),長軸長為
分別為左、右焦點(diǎn),長軸長為![]() 的橢圓(除去左、右頂點(diǎn)),可得動(dòng)點(diǎn)P的軌跡方程為
的橢圓(除去左、右頂點(diǎn)),可得動(dòng)點(diǎn)P的軌跡方程為![]()
(2)因?yàn)?/span>![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
所以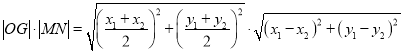
![]() .
.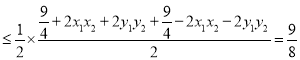
當(dāng)且僅當(dāng)![]() ,即
,即![]() 時(shí),等號成立,
時(shí),等號成立,
所以![]() 的最大值為
的最大值為![]() ,此時(shí)
,此時(shí)![]() ,即
,即![]() ,即
,即![]() 是直角三角形.
是直角三角形.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年某開發(fā)區(qū)一家汽車生產(chǎn)企業(yè)計(jì)劃引進(jìn)一批新能源汽車制造設(shè)備,通過市場分析,全年需投入固定成本3000萬元,每生產(chǎn)x(百輛),需另投入成本![]() 萬元,且
萬元,且 ,由市場調(diào)研知,每輛車售價(jià)6萬元,且全年內(nèi)生產(chǎn)的車輛當(dāng)年能全部銷售完.
,由市場調(diào)研知,每輛車售價(jià)6萬元,且全年內(nèi)生產(chǎn)的車輛當(dāng)年能全部銷售完.
(1)求出2019年的利潤![]() (萬元)關(guān)于年產(chǎn)量x(百輛)的函數(shù)關(guān)系式;(利潤=銷售額
(萬元)關(guān)于年產(chǎn)量x(百輛)的函數(shù)關(guān)系式;(利潤=銷售額![]() 成本)
成本)
(2)2019年產(chǎn)量為多少(百輛)時(shí),企業(yè)所獲利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】四邊形![]() 中,
中,![]() ,且
,且![]() ,
,![]() 為
為![]() 中點(diǎn),連接
中點(diǎn),連接![]() ,如圖(1),將其沿
,如圖(1),將其沿![]() 折起使得平面
折起使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,連接
,連接![]() ,如圖(2).
,如圖(2).
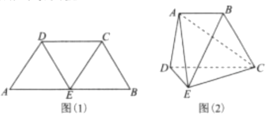
(1)證明:圖(2)中的![]() 四點(diǎn)共面;
四點(diǎn)共面;
(2)求圖(2)中平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】第28屆金雞百花電影節(jié)將于11月19日至23日在福建省廈門市舉辦,近日首批影展片單揭曉,《南方車站的聚會(huì)》《春江水暖》《第一次的離別》《春潮》《抵達(dá)之謎》五部優(yōu)秀作品將在電影節(jié)進(jìn)行展映.若從這五部作品中隨機(jī)選擇兩部放在展映的前兩位,則《春潮》與《抵達(dá)之謎》至少有一部被選中的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】江心洲有一塊如圖所示的江邊,![]() ,
,![]() 為岸邊,岸邊形成
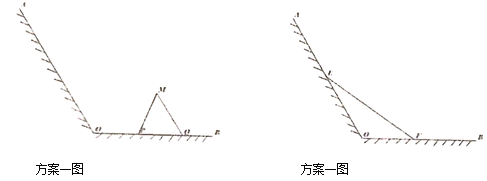
為岸邊,岸邊形成![]() 角,現(xiàn)擬在此江邊用圍網(wǎng)建一個(gè)江水養(yǎng)殖場,有兩個(gè)方案:方案l:在岸邊
角,現(xiàn)擬在此江邊用圍網(wǎng)建一個(gè)江水養(yǎng)殖場,有兩個(gè)方案:方案l:在岸邊![]() 上取兩點(diǎn)
上取兩點(diǎn)![]() ,用長度為
,用長度為![]() 的圍網(wǎng)依托岸邊線
的圍網(wǎng)依托岸邊線![]() 圍成三角形
圍成三角形![]() (
(![]() ,
,![]() 兩邊為圍網(wǎng));方案2:在岸邊
兩邊為圍網(wǎng));方案2:在岸邊![]() ,
,![]() 上分別取點(diǎn)
上分別取點(diǎn)![]() ,用長度為
,用長度為![]() 的圍網(wǎng)
的圍網(wǎng)![]() 依托岸邊圍成三角形
依托岸邊圍成三角形![]() .請分別計(jì)算
.請分別計(jì)算![]() ,
,![]() 面積的最大值,并比較哪個(gè)方案好.
面積的最大值,并比較哪個(gè)方案好.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義在R上的函數(shù)f(x)=|x﹣m|+|x|,m∈N*,存在實(shí)數(shù)x使f(x)<2成立.
(1)求實(shí)數(shù)m的值;
(2)若α≥1,β≥1,f(α)+f(β)=4,求證:![]() ≥3.
≥3.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() ,點(diǎn)E在BC上,
,點(diǎn)E在BC上,![]() .
.
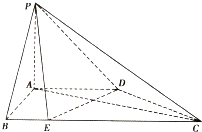
(1)求證:平面![]() 平面PAC;
平面PAC;
(2)若直線PE與平面PAC所成的角的正弦值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年2月13日《煙臺(tái)市全民閱讀促進(jìn)條例》全文發(fā)布,旨在保障全民閱讀權(quán)利,培養(yǎng)全民閱讀習(xí)慣,提高全民閱讀能力,推動(dòng)文明城市和文化強(qiáng)市建設(shè).某高校為了解條例發(fā)布以來全校學(xué)生的閱讀情況,隨機(jī)調(diào)查了200名學(xué)生每周閱讀時(shí)間![]() (單位:小時(shí))并繪制如圖所示的頻率分布直方圖.
(單位:小時(shí))并繪制如圖所示的頻率分布直方圖.

(1)求這200名學(xué)生每周閱讀時(shí)間的樣本平均數(shù)![]() 和中位數(shù)
和中位數(shù)![]() (
(![]() 的值精確到0.01);
的值精確到0.01);
(2)為查找影響學(xué)生閱讀時(shí)間的因素,學(xué)校團(tuán)委決定從每周閱讀時(shí)間為![]() ,
,![]() 的學(xué)生中抽取9名參加座談會(huì).
的學(xué)生中抽取9名參加座談會(huì).
(i)你認(rèn)為9個(gè)名額應(yīng)該怎么分配?并說明理由;
(ii)座談中發(fā)現(xiàn)9名學(xué)生中理工類專業(yè)的較多.請根據(jù)200名學(xué)生的調(diào)研數(shù)據(jù),填寫下面的列聯(lián)表,并判斷是否有![]() 的把握認(rèn)為學(xué)生閱讀時(shí)間不足(每周閱讀時(shí)間不足8.5小時(shí))與“是否理工類專業(yè)”有關(guān)?
的把握認(rèn)為學(xué)生閱讀時(shí)間不足(每周閱讀時(shí)間不足8.5小時(shí))與“是否理工類專業(yè)”有關(guān)?
閱讀時(shí)間不足8.5小時(shí) | 閱讀時(shí)間超過8.5小時(shí) | |
理工類專業(yè) | 40 | 60 |
非理工類專業(yè) |
附:![]() (
(![]() ).
).
臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| <> | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com