
科目: 來源: 題型:解答題
如圖,在四棱錐P-ABCD中,ABCD為平行四邊形,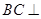 平面PAB,
平面PAB, ,
,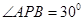 .M為PB的中點.
.M為PB的中點.
(1)求證:PD//平面AMC;
(2)求銳二面角B-AC-M的余弦值.
查看答案和解析>>
科目: 來源: 題型:解答題
如圖,在四棱錐 中,底面
中,底面 是矩形,
是矩形, ,
, ,
,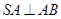 ,
, 是棱
是棱 的中點.
的中點.
(1)求證: 平面
平面 ;
;
(2)求證: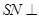 平面
平面 ;
;
(3)在棱 上是否存在一點
上是否存在一點 ,使得平面
,使得平面 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目: 來源: 題型:解答題
如圖1,在Rt△ABC中,∠ABC=90°,D為AC中點, 于
于 (不同于點
(不同于點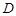 ),延長AE交BC于F,將△ABD沿BD折起,得到三棱錐
),延長AE交BC于F,將△ABD沿BD折起,得到三棱錐 ,如圖2所示.
,如圖2所示.
(1)若M是FC的中點,求證:直線 //平面
//平面 ;
;
(2)求證:BD⊥ ;
;
(3)若平面 平面
平面 ,試判斷直線
,試判斷直線 與直線CD能否垂直?并說明理由.
與直線CD能否垂直?并說明理由.
查看答案和解析>>
科目: 來源: 題型:解答題
已知四棱錐P-ABCD,底面ABCD是 ,邊長為
,邊長為 的菱形,又
的菱形,又 ,且PD=CD,點M、N分別是棱AD、PC的中點.
,且PD=CD,點M、N分別是棱AD、PC的中點.
(1)證明:DN//平面PMB;
(2)證明:平面PMB 平面PAD.
平面PAD.
查看答案和解析>>
科目: 來源: 題型:解答題
如圖,三棱柱 的底面是邊長為2的正三角形,且側棱垂直于底面,側棱長是,D是AC的中點。
的底面是邊長為2的正三角形,且側棱垂直于底面,側棱長是,D是AC的中點。
(1)求證: 平面
平面 ;
;
(2)求二面角 的大小;
的大小;
(3)求直線 與平面
與平面 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目: 來源: 題型:解答題
在四棱柱 中,
中, 底面
底面 ,底面
,底面 為菱形,
為菱形, 為
為 與
與 交點,已知
交點,已知 ,
, .
.
(1)求證: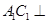 平面
平面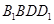 ;
;
(2)求證: ∥平面
∥平面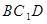 ;
;
(3)設點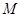 在
在 內(含邊界),且
內(含邊界),且
 ,說明滿足條件的點
,說明滿足條件的點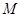 的軌跡,并求
的軌跡,并求 的最小值.
的最小值.
查看答案和解析>>
科目: 來源: 題型:解答題
已知多面體ABCDFE中, 四邊形ABCD為矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD, O、M分別為AB、FC的中點,且AB = 2,AD =" EF" = 1.
(1)求證:AF⊥平面FBC;
(2)求證:OM∥平面DAF;
(3)設平面CBF將幾何體EFABCD分成的兩個錐體的體積分別為VF-ABCD,VF-CBE,求VF-ABCD∶VF-CBE的值.
查看答案和解析>>
科目: 來源: 題型:解答題
如圖一,平面四邊形 關于直線
關于直線 對稱,
對稱,
 .把
.把 沿
沿 折起(如圖二),使二面角
折起(如圖二),使二面角 的余弦值等于
的余弦值等于 .對于圖二,完成以下各小題:
.對于圖二,完成以下各小題:
(1)求 兩點間的距離;
兩點間的距離;
(2)證明: 平面
平面 ;
;
(3)求直線 與平面
與平面 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com