日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

設數列{a_n}的各項都是正數，且對任意n∈N^*，都有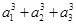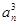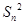＋…＋＝，記S_n為數列{a_n}的前n項和．
(1)求數列{a_n}的通項公式；
(2)若b_n＝3ⁿ＋(－1)^n－1λ·2a_n(λ為非零常數，n∈N^*)，問是否存在整數λ，使得對任意n∈N^*，都有b_n＋1>b_n.

已知{a_n}為等差數列，且a₂＝－1，a₅＝8.
(1)求數列{|a_n|}的前n項和；
(2)求數列{2ⁿ·a_n}的前n項和．

已知數列{a_n}的前n項和S_n滿足S_n＋a_n＋ ^n－1＝2(n∈N^*)，設c_n＝2ⁿa_n.
(1)求證：數列{c_n}是等差數列，并求數列{a_n}的通項公式．
(2)按以下規律構造數列{b_n}，具體方法如下：
b₁＝c₁，b₂＝c₂＋c₃，b₃＝c₄＋c₅＋c₆＋c₇，…，第n項b_n由相應的{c_n}中2^n－1項的和組成，求數列{b_n}的通項b_n. 

已知n∈N^*，數列{d_n}滿足d_n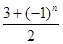＝，數列{a_n}滿足a_n＝d₁＋d₂＋d₃＋…＋d_2n，又知在數列{b_n}中，b₁＝2，且對任意正整數m，n，.
(1)求數列{a_n}和數列{b_n}的通項公式；
(2)將數列{b_n}中的第a₁項，第a₂項，第a₃項，…，第a_n項，…刪去后，剩余的項按從小到大的順序排成新數列{c_n}，求數列{c_n}的前2 013項和．

已知公差不為零的等差數列{a_n}的前4項和為10，且a₂，a₃，a₇成等比數列．
(1)求通項公式a_n；
(2)設b_n＝2a_n，求數列{b_n}的前n項和S_n.

已知單調遞增的等比數列{a_n}滿足：
a₂＋a₃＋a₄＝28，且a₃＋2是a₂和a₄的等差中項．
(1)求數列{a_n}的通項公式a_n；
(2)令b_n＝a_nlog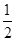a_n，S_n＝b₁＋b₂＋…＋b_n，求使S_n＋n·2^n＋1>50成立的最小的正整數n.

設數列{a_n}滿足a₁＝2，a₂＋a₄＝8，且對任意n∈N^*，函數f(x)＝(a_n－a_n＋1＋a_n＋2)x＋a_n＋1cos x－a_n＋2sin x滿足f′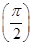＝0.
(1)求數列{a_n}的通項公式；
(2)若b_n＝2，求數列{b_n}的前n項和S_n.

在公差為d的等差數列{a_n}中，已知
a₁＝10，且a_1,2a₂＋2,5a₃成等比數列．
(1)求d，a_n；
(2)若d<0，求|a₁|＋|a₂|＋…＋|a_n|.

若正數項數列的前項和為，首項，點，在曲線上.
（1）求，；
（2）求數列的通項公式；
（3）設,表示數列的前項和，若恒成立，求及實數的取值范圍.

已知數列為等差數列，且 
（1）求數列的通項公式；
（2）證明：