
科目: 來源: 題型:解答題
已知函數 ,點
,點 、
、 在函數
在函數 的圖象上,
的圖象上,
點 在函數
在函數 的圖象上,設
的圖象上,設
 .
.
(1)求數列 的通項公式;
的通項公式;
(2)記 ,求數列
,求數列 的前
的前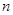 項和為
項和為 ;
;
(3)已知 ,記數列
,記數列 的前
的前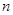 項和為
項和為 ,數列
,數列 的前
的前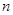 項和為
項和為 ,試比較
,試比較 與
與 的大小.
的大小.
查看答案和解析>>
科目: 來源: 題型:解答題
在一條筆直的工藝流水線上有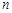 個工作臺,將工藝流水線用如圖
個工作臺,將工藝流水線用如圖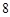 所示的數軸表示,各工作臺的坐標分別為
所示的數軸表示,各工作臺的坐標分別為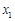 ,
,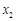 ,
,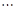 ,
,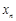 ,每個工作臺上有若干名工人.現要在流水線上建一個零件供應站,使得各工作臺上的所有工人到供應站的距離之和最短.
,每個工作臺上有若干名工人.現要在流水線上建一個零件供應站,使得各工作臺上的所有工人到供應站的距離之和最短.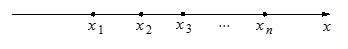
(Ⅰ)若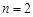 ,每個工作臺上只有一名工人,試確定供應站的位置;
,每個工作臺上只有一名工人,試確定供應站的位置;
(Ⅱ)若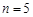 ,工作臺從左到右的人數依次為
,工作臺從左到右的人數依次為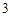 ,
,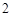 ,
,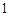 ,
,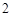 ,
,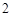 ,試確定供應站的位置,并求所有工人到供應站的距離之和的最小值.
,試確定供應站的位置,并求所有工人到供應站的距離之和的最小值.
查看答案和解析>>
科目: 來源: 題型:解答題
(14分)已知函數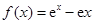 .
.
(Ⅰ)求函數 的最小值;
的最小值;
(Ⅱ)求證: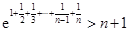
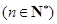 ;
;
(Ⅲ)對于函數 與
與 定義域上的任意實數
定義域上的任意實數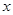 ,若存在常數
,若存在常數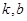 ,使得
,使得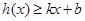 和
和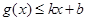 都成立,則稱直線
都成立,則稱直線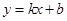 為函數
為函數 與
與 的“分界線”.設函數
的“分界線”.設函數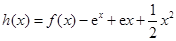 ,
,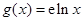 ,
, 與
與 是否存在“分界線”?若存在,求出
是否存在“分界線”?若存在,求出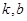 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:解答題
已知二次函數 的導函數的圖像與直線
的導函數的圖像與直線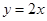 平行,且
平行,且 在
在 處取得極小值
處取得極小值 .設
.設 .
.
(1)若曲線 上的點
上的點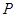 到點
到點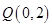 的距離的最小值為
的距離的最小值為 ,求
,求 的值;
的值;
(2)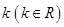 如何取值時,函數
如何取值時,函數 存在零點,并求出零點.
存在零點,并求出零點.
查看答案和解析>>
科目: 來源: 題型:解答題
為了在夏季降溫和冬季供暖時減少能源消耗,房屋的屋頂和外墻需要建造隔熱層,某棟建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元.該建筑物每年的能源消耗費用 (單位:萬元)與隔熱層厚度
(單位:萬元)與隔熱層厚度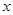 (單位:
(單位: )滿足關系:
)滿足關系:
若不建隔熱層,每年能源消耗費用為8萬元。設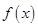 為隔熱層建造費用與20年的能源消耗費用之和。
為隔熱層建造費用與20年的能源消耗費用之和。
(Ⅰ)求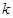 的值及
的值及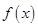 的表達式;
的表達式;
(Ⅱ)隔熱層修建多厚時,總費用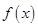 最小,并求最小值.
最小,并求最小值.
查看答案和解析>>
科目: 來源: 題型:解答題
對于函數 ,若存在實數對(
,若存在實數對( ),使得等式
),使得等式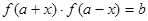 對定義域中的每一個
對定義域中的每一個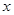 都成立,則稱函數
都成立,則稱函數 是“(
是“( )型函數”.
)型函數”.
(Ⅰ)判斷函數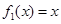 是否為 “(
是否為 “( )型函數”,并說明理由;
)型函數”,并說明理由;
(Ⅱ)若函數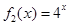 是“(
是“( )型函數”,求出滿足條件的一組實數對
)型函數”,求出滿足條件的一組實數對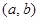 ;,
;,
(Ⅲ)已知函數 是“(
是“( )型函數”,對應的實數對
)型函數”,對應的實數對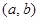 為
為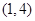 .當
.當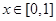 時,
時,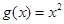
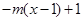
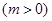 ,若當
,若當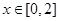 時,都有
時,都有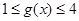 ,試求
,試求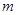 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:解答題
提高過江大橋的車輛通行能力可改善整個城市的交通狀況.在一般情況下,大橋上的車流速度v(單位:千米/小時)是車流密度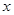 (單位:輛/千米)的函數.當橋上的的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時,研究表明:當
(單位:輛/千米)的函數.當橋上的的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時,研究表明:當 時,車流速度
時,車流速度 是車流密度x的一次函數.
是車流密度x的一次函數.
(Ⅰ)當 時,求函數
時,求函數 的表達式;
的表達式;
(Ⅱ)當車流密度 為多大時,車流量(單位時間內通過橋上某觀察點的車輛數,單位:輛/每小時)
為多大時,車流量(單位時間內通過橋上某觀察點的車輛數,單位:輛/每小時) 可以達到最大,并求出最大值(精確到1輛/小時).
可以達到最大,并求出最大值(精確到1輛/小時).
查看答案和解析>>
科目: 來源: 題型:解答題
某企業生產某種商品 噸,此時所需生產費用為(
噸,此時所需生產費用為(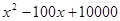 )萬元,當出售這種商品時,每噸價格為
)萬元,當出售這種商品時,每噸價格為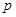 萬元,這里
萬元,這里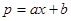 (
(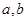 為常數,
為常數,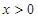 )
)
(1)為了使這種商品的生產費用平均每噸最低,那么這種商品的產量應為多少噸?
(2)如果生產出來的商品能全部賣完,當產量是120噸時企業利潤最大,此時出售價格是每噸160萬元,求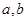 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com