日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

如圖，三棱錐A－BPC中，AP⊥PC，AC⊥BC，M為AB中點，D為PB中點，且△PMB為正三角形．

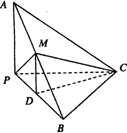
(1)求證：DM∥平面APC；

(2)求證：平面ABC⊥平面APC；

(3)若BC＝4，AB＝20，求三棱錐D－BCM的體積．

設函數f(x)＝ax＋(x－1)，若a是從1，2，3三個數中任取一個數，b是從2，3，4，5四個數中任取一個數，求f(x)＞b恒成立的概率．

△ABC的三個內角A，B，C所對的邊分別為a，b，c，向量＝(－1，1)，＝(cosBcosC，sinBsinC－)，且⊥．

(1)求A的大小；

(2)現在給出下列三個條件：①a＝1；②2c－(＋1)b＝0；③B＝45°，試從中選擇兩個條件以確定△ABC，求出所確定的△ABC的面積．(注：只需要選擇一種方案答題，如果用多種方案答題，則按第一方案給分)．

在極坐標系中，O為極點，半徑為2的圓C的圓心的極坐標為(2，)．

(1)求圓C的極坐標方程；

(2)P是圓C上一動點，點Q滿足3＝，以極點O為原點，以極軸為x軸正半軸建立直角坐標系，求點Q的軌跡的直角坐標方程．

如圖，AB、CD是圓的兩條平行弦，BE∥AC，BE交CD于E、交圓于F，過A點的切線交DC的延長線于P，PC＝ED＝1，PA＝2．

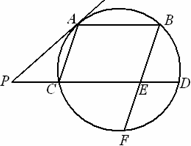
(Ⅰ)求AC的長；

(Ⅱ)求證：BE＝EF．

設函數．

(Ⅰ)求f(x)的單調區間和極值；

(Ⅱ)是否存在實數a，使得關于x的不等式f(x)≥0的解集為(0，＋∞)？若存在，求a的取值范圍；若不存在，試說明理由．

設橢圓E：(a，b＞0)過M(2，)，N(，1)兩點，O為坐標原點，

(Ⅰ)求橢圓E的方程；

(Ⅱ)是否存在圓心在原點的圓，使得該圓的任意一條切線與橢圓E恒有兩個交點A，B，且⊥？若存在，寫出該圓的方程，并求|AB|的取值范圍，若不存在說明理由．

如圖，在底面為直角梯形的四棱錐P－ABCD中AD∥BC，∠ABC＝90°，PD⊥平面ABCD，AD＝1，AB＝，BC＝4．

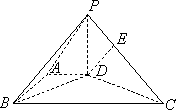
(1)求證：BD⊥PC；

(2)求直線AB與平面PDC所成的角；

(3)設點E在棱PC上，＝λ，若DE∥平面PAB，求λ的值．

符合下列三個條件之一，某名牌大學就可錄取：

①獲國家高中數學聯賽一等獎(保送錄取，聯賽一等獎從省高中數學競賽優勝者中考試選拔)；

②自主招生考試通過并且高考分數達到一本分數線(只有省高中數學競賽優勝者才具備自主招生考試資格)；

③高考分數達到該大學錄取分數線(該大學錄取分數線高于一本分數線)．

某高中一名高二數學尖子生準備報考該大學，他計劃：若獲國家高中數學聯賽一等獎，則保送錄取；若未被保送錄取，則再按條件②、條件③的順序依次參加考試．

已知這名同學獲省高中數學競賽優勝獎的概率是0.9，通過聯賽一等獎選拔考試的概率是0.5，通過自主招生考試的概率是0.8，高考分數達到一本分數線的概率是0.6，高考分數達到該大學錄取分數線的概率是0.3.

(Ⅰ)求這名同學參加考試次數ξ的分布列及數學期望；

(Ⅱ)求這名同學被該大學錄取的概率．

對于給定數列{a_n}，如果存在實常數p，q，使得a_n+1＝pa_n＋q對于任意n∈N^*都成立，我們稱數列{a_n}是“M類數列”．

(Ⅰ)已知數列{b_n}是“M類數列”且b_n＝2n，求它對應的實常數p，q的值；

(Ⅱ)若數列{c_n}滿足c₁＝1，c_n+1－c_n＝2ⁿ(n∈N^*)，求數列{c_n}的通項公式．并判斷{c_n}是否為“M類數列”，說明理由．