相關習題
0 110323 110331 110337 110341 110347 110349 110353 110359 110361 110367 110373 110377 110379 110383 110389 110391 110397 110401 110403 110407 110409 110413 110415 110417 110418 110419 110421 110422 110423 110425 110427 110431 110433 110437 110439 110443 110449 110451 110457 110461 110463 110467 110473 110479 110481 110487 110491 110493 110499 110503 110509 110517 266669
科目:
來源:2010年廣東省高考數學沖刺預測試卷15(理科)(解析版)
題型:解答題
設函數f(x)=|x-a|-2,若不等式|f(x)|<1的解x∈(-2,0)∪(2,4),則實數a= .
查看答案和解析>>
科目:
來源:2010年廣東省高考數學沖刺預測試卷15(理科)(解析版)
題型:解答題
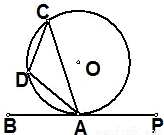
如圖,已知PB是⊙O的切線,A是切點,D是弧AC上一點,若∠BAC=70°,則∠ADC=
.
查看答案和解析>>
科目:
來源:2010年廣東省高考數學沖刺預測試卷15(理科)(解析版)
題型:解答題
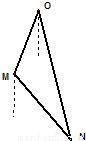
如圖所示,正在亞丁灣執行護航任務的某導彈護衛艦,突然收到一艘商船的求救信號,緊急前往相關海域.到達相關海域O處后發現,在南偏西20°、5海里外的洋面M處有一條海盜船,它正以每小時20海里的速度向南偏東40°的方向逃竄.某導彈護衛艦當即施放載有突擊隊員的快艇進行攔截,快艇以每小時30海里的速度向南偏東θ°的方向全速追擊.請問:快艇能否追上海盜船?如果能追上,請求出sin(θ°+20°)的值;如果未能追上,請說明理由.(假設海面上風平浪靜、海盜船逃竄的航向不變、快艇運轉正常無故障等)
查看答案和解析>>
科目:
來源:2010年廣東省高考數學沖刺預測試卷15(理科)(解析版)
題型:解答題
某商場經銷某商品,根據以往資料統計,顧客采用的付款期數ξ的分布列為
商場經銷一件該商品,采用1期付款,其利潤為200元;分2期或3期付款,其利潤為250元;分4期或5期付款,其利潤為300元,η表示經銷一件該商品的利潤.
(Ⅰ)求事件A:“購買該商品的3位顧客中,至少有1位采用1期付款”的概率P(A);
(Ⅱ)求η的分布列及期望Eη.
查看答案和解析>>
科目:
來源:2010年廣東省高考數學沖刺預測試卷15(理科)(解析版)
題型:解答題
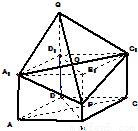
如圖,已知直四棱柱ABCD-A
1B
1C
1D
1的底面是邊長為2、∠ADC=120°的菱形,Q是側棱DD
1(DD
1>
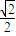
)延長線上的一點,過點Q、A
1、C
1作菱形截面QA
1PC
1交側棱BB
1于點P.設截面QA
1PC
1的面積為S
1,四面體B
1-A
1C
1P的三側面△B
1A
1C
1、△B
1PC
1、△B
1A
1P面積的和為S
2,S=S
1-S
2.
(Ⅰ)證明:AC⊥QP;
(Ⅱ)當S取得最小值時,求cos∠A
1QC
1的值.
查看答案和解析>>
科目:
來源:2010年廣東省高考數學沖刺預測試卷15(理科)(解析版)
題型:解答題
在直角坐標平面內,定點F(-1,0)、F′(1,0),動點M,滿足條件
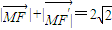
.
(Ⅰ)求動點M的軌跡C的方程;
(Ⅱ)過點F的直線交曲線C交于A,B兩點,求以AB為直徑的圓的方程,并判定這個圓與直線x=-2的位置關系.
查看答案和解析>>
科目:
來源:2010年廣東省高考數學沖刺預測試卷15(理科)(解析版)
題型:解答題
已知數列{an}的前n項和Sn=2an-3•2n+4,n=1,2,3,….
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)設Tn為數列{Sn-4}的前n項和,求Tn.
查看答案和解析>>
科目:
來源:2010年廣東省高考數學沖刺預測試卷15(理科)(解析版)
題型:解答題
函數f(x)=x
3-6x
2的定義域為[-2,t],設f(-2)=m,f(t)=n,f′(x)是f(x)的導數.
(Ⅰ)求證:n≥m;
(Ⅱ)確定t的范圍使函數f(x)在[-2,t]上是單調函數;
(Ⅲ)求證:對于任意的t>-2,總存在x
∈(-2,t),滿足
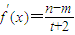
;并確定這樣的x
的個數.
查看答案和解析>>
科目:
來源:廣東省高考數學一輪復習:4.2 利用導數研究函數的單調性(解析版)
題型:選擇題
函數y=x+xln x的單調遞減區間是( )
A.(-∞,e-2)
B.(0,e-2)
C.(e-2,+∞)
D.(e2,+∞)
查看答案和解析>>
科目:
來源:廣東省高考數學一輪復習:4.2 利用導數研究函數的單調性(解析版)
題型:選擇題
設f(x)、g(x)是R上的可導函數,f′(x),g′(x)分別為f(x)、g(x)的導函數,且滿足f′(x)g(x)+f(x)g′(x)<0,則當a<x<b時,有( )
A.f(x)g(b)>f(b)g(x)
B.f(x)g(a)>f(a)g(x)
C.f(x)g(x)>f(b)g(b)
D.f(x)g(x)>f(b)g(a)
查看答案和解析>>

 如圖,已知PB是⊙O的切線,A是切點,D是弧AC上一點,若∠BAC=70°,則∠ADC= .
如圖,已知PB是⊙O的切線,A是切點,D是弧AC上一點,若∠BAC=70°,則∠ADC= .
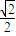 )延長線上的一點,過點Q、A1、C1作菱形截面QA1PC1交側棱BB1于點P.設截面QA1PC1的面積為S1,四面體B1-A1C1P的三側面△B1A1C1、△B1PC1、△B1A1P面積的和為S2,S=S1-S2.
)延長線上的一點,過點Q、A1、C1作菱形截面QA1PC1交側棱BB1于點P.設截面QA1PC1的面積為S1,四面體B1-A1C1P的三側面△B1A1C1、△B1PC1、△B1A1P面積的和為S2,S=S1-S2.
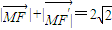 .
.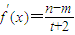 ;并確定這樣的x的個數.
;并確定這樣的x的個數.