
【題目】已知函數(shù)![]() 的極小值為0.
的極小值為0.
(1)求實數(shù)![]() 的值;
的值;
(2)若不等式![]() 對任意
對任意![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)由極小值的定義知道,只需要令![]() ,解得
,解得![]() ,且描述
,且描述![]() 兩側(cè)的單調(diào)性;(2)原式子轉(zhuǎn)化為
兩側(cè)的單調(diào)性;(2)原式子轉(zhuǎn)化為![]() 在
在![]() 上恒成立;求導
上恒成立;求導![]() ,研究導函數(shù)的正負即可,從而得到函數(shù)的單調(diào)性和最值即可。
,研究導函數(shù)的正負即可,從而得到函數(shù)的單調(diào)性和最值即可。
(1)∵![]() ,令
,令![]() ,解得
,解得![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,故
上單調(diào)遞增,故![]() 的極小值為
的極小值為![]() ,
,
由題意有![]() ,解得
,解得![]() .
.
(2)由(1)知不等式![]() 對任意
對任意![]() 恒成立,∵
恒成立,∵![]() ,∴
,∴![]() 在
在![]() 上恒成立,∵不妨設(shè)
上恒成立,∵不妨設(shè)![]() ,
, ![]() ,則
,則![]() .
.
當![]() 時,
時, ![]() ,故
,故![]() ,∴
,∴![]() 在
在![]() 上單調(diào)遞增,從而
上單調(diào)遞增,從而![]() ,∴
,∴![]() 不成立.當
不成立.當![]() 時,令
時,令![]() ,解得
,解得![]() ,若
,若![]() ,即
,即![]() ,當
,當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上為增函數(shù),故
上為增函數(shù),故![]() ,不合題意;若
,不合題意;若![]() ,即
,即![]() ,當
,當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上為減函數(shù),故
上為減函數(shù),故![]() ,符合題意.綜上所述,
,符合題意.綜上所述, ![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數(shù)學 來源: 題型:
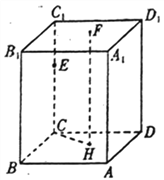
【題目】如圖所示,直平行六面體![]() 中,
中,![]() 為棱
為棱![]() 上任意一點,
上任意一點,![]() 為底面
為底面![]() (除
(除![]() 外)上一點,已知
外)上一點,已知![]() 在底面
在底面![]() 上的射影為
上的射影為![]() ,若再增加一個條件,就能得到
,若再增加一個條件,就能得到![]() ,現(xiàn)給出以下條件:
,現(xiàn)給出以下條件:
①![]() ;②
;②![]() 在
在![]() 上;③
上;③![]() 平面
平面![]() ;④直線
;④直線![]() 和
和![]() 在平面
在平面![]() 的射影為同一條直線.其中一定能成為增加條件的是__________.(把你認為正確的都填上)
的射影為同一條直線.其中一定能成為增加條件的是__________.(把你認為正確的都填上)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某廠生產(chǎn)某產(chǎn)品的年固定成本為250萬元,每生產(chǎn)![]() 千件,需另投入成本
千件,需另投入成本![]() (萬元),若年產(chǎn)量不足
(萬元),若年產(chǎn)量不足![]() 千件,
千件, ![]() 的圖像是如圖的拋物線,此時
的圖像是如圖的拋物線,此時![]() 的解集為
的解集為![]() ,且
,且![]() 的最小值是
的最小值是![]() ,若年產(chǎn)量不小于
,若年產(chǎn)量不小于![]() 千件,
千件, ![]() ,每千件商品售價為50萬元,通過市場分析,該廠生產(chǎn)的商品能全部售完;
,每千件商品售價為50萬元,通過市場分析,該廠生產(chǎn)的商品能全部售完;
(1)寫出年利潤![]() (萬元)關(guān)于年產(chǎn)量
(萬元)關(guān)于年產(chǎn)量![]() (千件)的函數(shù)解析式;
(千件)的函數(shù)解析式;
(2)年產(chǎn)量為多少千件時,該廠在這一商品的生產(chǎn)中所獲利潤最大?

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為矩形,側(cè)面
為矩形,側(cè)面![]() 為正三角形,且平面
為正三角形,且平面![]()
![]() 平面,
平面, ![]() 為
為![]() 中點,
中點, ![]() .
.

(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若二面角![]() 的平面角大小
的平面角大小![]() 滿足
滿足![]() ,求四棱錐
,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在平面直角坐標系![]() 中,傾斜角為
中,傾斜角為![]() 的直線
的直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).以坐標原點為極點,以
為參數(shù)).以坐標原點為極點,以![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() .若點
.若點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 經(jīng)過點
經(jīng)過點![]() 且與曲線
且與曲線![]() 相交于
相交于![]() 兩點,設(shè)線段
兩點,設(shè)線段![]() 的中點為
的中點為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某企業(yè)生產(chǎn)A、B、C三種家電,經(jīng)市場調(diào)查決定調(diào)整生產(chǎn)方案,計劃本季度(按不超過480個工時計算)生產(chǎn)A、B、C三種家電共120臺,其中A家電至少生產(chǎn)20臺,已知生產(chǎn)A、B、C三種家電每臺所需的工時分別為3、4、6個工時,每臺的產(chǎn)值分別為20、30、40千元,則按此方案生產(chǎn),此季度最高產(chǎn)值為( )千元.
A. 3600 B. 350 C. 4800 D. 480
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知定義域為R的函數(shù)f(x)= ![]() 是奇函數(shù),f(1)=﹣
是奇函數(shù),f(1)=﹣ ![]() .
.
(1)求a,b的值;
(2)判斷函數(shù)f(x)的單調(diào)性,并用定義證明.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() .
.
(Ⅰ)若曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直,求函數(shù)
垂直,求函數(shù)![]() 的極值;
的極值;
(Ⅱ)設(shè)函數(shù)![]() .當
.當![]() 時,若區(qū)間
時,若區(qū)間![]() 上存在
上存在![]() ,使得
,使得![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.(
的取值范圍.(![]() 為自然對數(shù)底數(shù))
為自然對數(shù)底數(shù))
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com