
���}Ŀ����֪�E�A![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ��
��![]() ���^�c(di��n)
���^�c(di��n)![]() ��ֱ��
��ֱ��![]() �c�E�A
�c�E�A![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)��
���c(di��n)��
��1����(d��ng)ֱ��![]() ��б��
���![]() �r(sh��)����
�r(sh��)����![]() ����e��
����e��
��2����(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ��ȡֵ������
��ȡֵ������
���𰸡���1��![]() ����2��
����2��![]() .
.
��������
��1���ȸ���(j��)�E�A�Ď����|(zh��)���![]() ��
��![]() ������(bi��o)���M(j��n)�������ֱ��
������(bi��o)���M(j��n)�������ֱ��![]() �ķ��̣�Ȼ��(li��n)�����̣��Y(ji��)�ϸ��cϵ��(sh��)���P(gu��n)ϵ�������
�ķ��̣�Ȼ��(li��n)�����̣��Y(ji��)�ϸ��cϵ��(sh��)���P(gu��n)ϵ�������![]() ����e��
����e��
��2�������}��õ�ֱ��![]() ��б�ʲ����ڕr(sh��)���M���}�⣬���O(sh��)��ֱ��
��б�ʲ����ڕr(sh��)���M���}�⣬���O(sh��)��ֱ��![]() �ķ��̣��c�E�A����(li��n)��������(j��)�l�����
�ķ��̣��c�E�A����(li��n)��������(j��)�l�����![]() ��ȡֵ������������ÓQԪ�����
��ȡֵ������������ÓQԪ�����![]() ��ȡֵ�������ɣ�
��ȡֵ�������ɣ�
��1���əE�A![]() ���ɵ����ҽ��c(di��n)�քe��
���ɵ����ҽ��c(di��n)�քe��![]() ��
��![]() ��
��
��?y��n)�ֱ��![]() ��б��
��б��![]() ������ֱ��
������ֱ��![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() ��
��
(li��n)�����̣���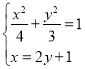 ����ȥ
����ȥ![]() ������(ji��n)��������
������(ji��n)��������![]() ��
��
�O(sh��)![]() ��
��![]() ���t
���t![]() ��
��![]() ��
��
����![]() ����
����![]() ����e��
����e��![]() ��
��
��2����(d��ng)ֱ��![]() ��б�ʲ����ڕr(sh��)��ֱ��
��б�ʲ����ڕr(sh��)��ֱ��![]() �ķ��̞�
�ķ��̞�![]() �����Բ����O(sh��)
�����Բ����O(sh��)![]() ��
��![]() ��
��
�ɵ�![]() �����M��
�����M��![]() ��
��
����ֱ��![]() ��б�ʴ��ڣ��O(sh��)ֱ��
��б�ʴ��ڣ��O(sh��)ֱ��![]() ��
��
(li��n)�����̣��� ����ȥ
����ȥ![]() ��
��![]() ��
��
![]() ��
��
�O(sh��)![]() ��
��![]() ���t
���t![]() ��
��![]() ��
��
����![]()
![]()
![]()
![]()
![]()
![]() ��
��
����![]() �����
�����![]() ��
��
�ɵ�![]()
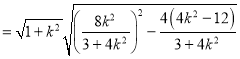
![]() ��
��
��![]() ���t
���t![]() ���ɵ�
���ɵ� ��
��
��?y��n)?/span>![]() ������
������![]() ��
��
��![]() ��ȡֵ������
��ȡֵ������![]() ��
��


 ꖹ��n��ͬ������(x��)ϵ�д�
ꖹ��n��ͬ������(x��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ij���(gu��)�Z�W(xu��)У�e�е�![]() (��������(sh��)�W(xu��)��ģ��ِ)��,���c��ِ��Ů���c�����˔�(sh��)֮�Ȟ�
(��������(sh��)�W(xu��)��ģ��ِ)��,���c��ِ��Ů���c�����˔�(sh��)֮�Ȟ�![]() ,�ҳɿ�(j��)�ֲ���
,�ҳɿ�(j��)�ֲ���![]() ,��?j��n)?sh��)��
,��?j��n)?sh��)��![]() ����(��
����(��![]() )��ͬ�W(xu��)�@��(ji��ng)����Ů���������÷ӳ�ӵķ�����ȡ
)��ͬ�W(xu��)�@��(ji��ng)����Ů���������÷ӳ�ӵķ�����ȡ![]() �˵ijɿ�(j��)����ӱ�,�õ��ɿ�(j��)���l�ʷֲ�ֱ���D��D��ʾ��
�˵ijɿ�(j��)����ӱ�,�õ��ɿ�(j��)���l�ʷֲ�ֱ���D��D��ʾ��
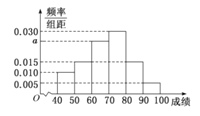
(��)��![]() ��ֵ,��Ӌ(j��)������ȡ�ӱ���ƽ��ֵ
��ֵ,��Ӌ(j��)������ȡ�ӱ���ƽ��ֵ![]() (ͬһ�M�еĔ�(sh��)��(j��)��ԓ�M�^(q��)�g�����c(di��n)ֵ������)��
(ͬһ�M�еĔ�(sh��)��(j��)��ԓ�M�^(q��)�g�����c(di��n)ֵ������)��
(��)������![]() ��(li��n)��,���Д��ڷ��e(cu��)�`�ĸ��ʲ����^
��(li��n)��,���Д��ڷ��e(cu��)�`�ĸ��ʲ����^![]() ��ǰ�����ܷ��J(r��n)�顰�@��(ji��ng)�cŮ�����������P(gu��n)����
��ǰ�����ܷ��J(r��n)�顰�@��(ji��ng)�cŮ�����������P(gu��n)����
Ů�� | ���� | ��Ӌ(j��) | |
�@��(ji��ng) |
| ||
���@��(ji��ng) | |||
��Ӌ(j��) |
| ||
��������ʽ��
|
|
|
|
|
|
|
|
|
|
|
|
|
|
����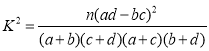 ,
,![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У���֪�E�A
�У���֪�E�A![]() ������c(di��n)��
������c(di��n)��![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)��![]() ��
��![]() ��
��![]() ��E�A
��E�A![]() �σ��c(di��n)���A
�σ��c(di��n)���A![]() .
.
��1����![]() �S���ҝM��ֱ��
�S���ҝM��ֱ��![]() �c�A
�c�A![]() ������A
���У���A![]() �ķ��̣�
�ķ��̣�
��2����A![]() �İ돽��2���c(di��n)
�İ돽��2���c(di��n)![]() ��
��![]() �M��
�M��![]() ����ֱ��
����ֱ��![]() ���A
���A![]() �ص����L(zh��ng)�����ֵ.
�ص����L(zh��ng)�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��2020���¹ڷ������鱩�l(f��)�ԁ����Ї�(gu��)����Ѹ�ٲ�ȡ��ȫ�桢���(y��n)����صķ����e�룬��(ji��n)�Q�����������ӄ�(sh��)�^��Ŭ��������Ӱ푽�����ͣ���ȫ���翹���¹ڷ�������������ؕ�I(xi��n)�����ռ������¹ڷ������P(gu��n)֪�R(sh��)��ij���ЌW(xu��)У�_չ�˾����¹ڷ�����֪�R(sh��)��(j��ng)����(d��ng)���F(xi��n)�Ĵ������c�����S�C(j��)��ȡ200�����\(y��n)�ߣ������ĵ÷֣��M��100�֣���(sh��)��(j��)�y(t��ng)Ӌ(j��)�Y(ji��)����D��
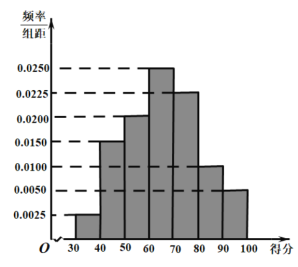
��1�����˴�֪�R(sh��)��(j��ng)��÷�![]() ���w�������B(t��i)�ֲ����Øӱ�����Ӌ(j��)���w���O(sh��)
���w�������B(t��i)�ֲ����Øӱ�����Ӌ(j��)���w���O(sh��)![]() ��
��![]() �քe���@200�����\(y��n)�ߵ÷ֵ�ƽ��ֵ�͘�(bi��o)��(zh��n)�ͬһ�M��(sh��)��(j��)��ԓ�^(q��)�g���c(di��n)ֵ���棩����
�քe���@200�����\(y��n)�ߵ÷ֵ�ƽ��ֵ�͘�(bi��o)��(zh��n)�ͬһ�M��(sh��)��(j��)��ԓ�^(q��)�g���c(di��n)ֵ���棩����![]() ��
��![]() ��ֵ��
��ֵ��![]() ��
��![]() ��ֵ��������ȡ����(sh��)������Ӌ(j��)��
��ֵ��������ȡ����(sh��)������Ӌ(j��)��![]() ��
��
��2���ڣ�1���ėl���£�����x��ҷe�O���c�@�λ��(d��ng)����(du��)���c�˴�֪�R(sh��)��(j��ng)������\(y��n)���ƶ����ª�(ji��ng)��(l��)�������÷ֵ���![]() �ī@��1�γ骄(ji��ng)�C(j��)��(hu��)���÷ֲ�����
�ī@��1�γ骄(ji��ng)�C(j��)��(hu��)���÷ֲ�����![]() �ī@��2�γ骄(ji��ng)�C(j��)��(hu��)���ٶ�ÿ�γ骄(ji��ng)�У��鵽18Ԫ�t���ĸ��ʞ�
�ī@��2�γ骄(ji��ng)�C(j��)��(hu��)���ٶ�ÿ�γ骄(ji��ng)�У��鵽18Ԫ�t���ĸ��ʞ�![]() ���鵽36Ԫ�t���ĸ��ʞ�
���鵽36Ԫ�t���ĸ��ʞ�![]() ����֪����ijͬ�W(xu��)���@�λ��(d��ng)�е����\(y��n)�ߣ�ӛ
����֪����ijͬ�W(xu��)���@�λ��(d��ng)�е����\(y��n)�ߣ�ӛ![]() ��ԓͬ�W(xu��)�ڳ骄(ji��ng)�Ы@�üt���Ŀ����~����
��ԓͬ�W(xu��)�ڳ骄(ji��ng)�Ы@�üt���Ŀ����~����![]() �ķֲ��к͔�(sh��)�W(xu��)�������������e�k�˴λ��(d��ng)����Ҫ�骄(ji��ng)�t���Ŀ����~��
�ķֲ��к͔�(sh��)�W(xu��)�������������e�k�˴λ��(d��ng)����Ҫ�骄(ji��ng)�t���Ŀ����~��
������(sh��)��(j��)��![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����(du��)�ڽo���Ĕ�(sh��)��![]() ��
��![]() ���O(sh��)
���O(sh��)![]() ����
����![]() ��
��![]() ��
��![]() ������
������![]() �е����ֵ���t�Q��(sh��)��
�е����ֵ���t�Q��(sh��)��![]() �ǔ�(sh��)��
�ǔ�(sh��)��![]() ��
��![]() �ġ����C��(sh��)�С���
�ġ����C��(sh��)�С���
��1���O(sh��)![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��ֵ�����C����(sh��)��
��ֵ�����C����(sh��)��![]() �ǵȲ(sh��)�У�
�ǵȲ(sh��)�У�
��2���O(sh��)��(sh��)��![]() ��
��![]() ���ǹ��Ȟ�q�����(xi��ng)�ȱȔ�(sh��)�У�����(sh��)��
���ǹ��Ȟ�q�����(xi��ng)�ȱȔ�(sh��)�У�����(sh��)��![]() �ǵȲ(sh��)�У���q��ȡֵ������
�ǵȲ(sh��)�У���q��ȡֵ������
��3���O(sh��)��(sh��)��![]() �M��
�M��![]() ����(sh��)��
����(sh��)��![]() �ǔ�(sh��)��
�ǔ�(sh��)��![]() ��
��![]() �ġ����C��(sh��)�С�����
�ġ����C��(sh��)�С�����![]() ��m�鳣��(sh��)��
��m�鳣��(sh��)��![]() ��2������k�������C��
��2������k�������C��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D�����L(zh��ng)���w![]() �У�
��![]() ��
��![]() �����c(di��n)���c(di��n)
�����c(di��n)���c(di��n)![]() ��
��![]() ��һ�c(di��n)��
��һ�c(di��n)��![]() ��
��![]() ��
��![]() .��(d��ng)�c(di��n)
.��(d��ng)�c(di��n)![]() ���ϵ���
���ϵ���![]() �ϣ��ҝM�������F
�ϣ��ҝM�������F![]() ���w�e����1���tֱ��
���w�e����1���tֱ��![]() �c
�c![]() ���ɽǵ�����ֵ�����ֵ�飨 ��
���ɽǵ�����ֵ�����ֵ�飨 ��

A.![]() B.
B.![]() C.
C.![]() D.2
D.2
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() .����
.����![]() ��
��
��1����![]() .���C��
.���C��![]() .
.
��2��������ʽ![]() ��(du��)
��(du��)![]() �������ԇ��
�������ԇ��![]() ��ȡֵ����
��ȡֵ����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ��������c(di��n)�քe��A��B���x���ʞ�
��������c(di��n)�քe��A��B���x���ʞ�![]() ���L(zh��ng)�S�L(zh��ng)��4����(d��ng)�c(di��n)S��C��λ��x�S�Ϸ���ֱ��
���L(zh��ng)�S�L(zh��ng)��4����(d��ng)�c(di��n)S��C��λ��x�S�Ϸ���ֱ��![]() �cֱ��
�cֱ��![]() ���քe����M��N���c(di��n).
���քe����M��N���c(di��n).
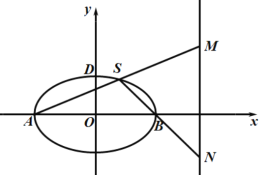
��1����E�AC�ķ���
��2����|MN|����Сֵ
��3����(d��ng)![]() ��С�r(sh��)���ڙE�AC���Ƿ�����@�ӵ��c(di��n)T��ʹ��TSB��e��
��С�r(sh��)���ڙE�AC���Ƿ�����@�ӵ��c(di��n)T��ʹ��TSB��e��![]() �������ڣ�Ո(q��ng)�_���c(di��n)T�Ă�(g��)��(sh��)���������ڣ�Ո(q��ng)�f������
�������ڣ�Ո(q��ng)�_���c(di��n)T�Ă�(g��)��(sh��)���������ڣ�Ո(q��ng)�f������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����ƽ��ֱ������(bi��o)ϵxOy�У��E�A![]() ���ҽ��c(di��n)������c(di��n)�քe��F��A���^ԭ�c(di��n)��ֱ���c�E�AC�����c(di��n)P��Q���c(di��n)P�ڵ�һ���ރ�(n��i)�����B�Y(ji��)PA��QF����
���ҽ��c(di��n)������c(di��n)�քe��F��A���^ԭ�c(di��n)��ֱ���c�E�AC�����c(di��n)P��Q���c(di��n)P�ڵ�һ���ރ�(n��i)�����B�Y(ji��)PA��QF����![]() ��
��![]() ����e��
����e��![]() ��e��3����
��e��3����
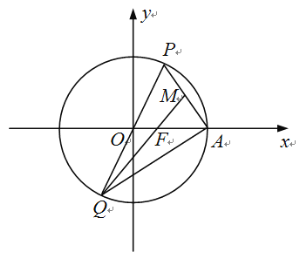
��1����E�AC�Ę�(bi��o)��(zh��n)���̣�
��2����֪M�龀��PA�����c(di��n)���B�Y(ji��)QA��QM��
�����C��Q��F��M���c(di��n)������
��ӛֱ��QP��QM��QA��б�ʷքe��![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ����e��
����e��
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com