【題目】西北某省會城市計劃新修一座城市運動公園，設計平面如圖所示：其為五邊形
，其中三角形區域
為球類活動場所；四邊形
為文藝活動場所，
，為運動小道（不考慮寬度）
，
，
千米.
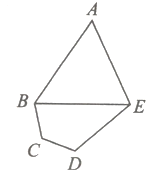
（1）求小道
的長度；
（2）求球類活動場所
的面積最大值.
七星圖書口算速算天天練系列答案
初中學業考試導與練系列答案科目：高中數學 來源： 題型：
【題目】某海濱浴場一天的海浪高度
是時間
的函數，記作
，下表是某天各時的浪高數據：
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
（1）選用一個三角函數來近似描述這個海濱浴場的海浪高度與時間
的函數關系；
（2）依據規定，當海浪高度不少于
時才對沖浪愛好者開放海濱浴場，請依據（1）的結論，判斷一天內的
至
之間，有多少時間可供沖浪愛好者進行沖浪？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在極坐標系中，曲線
：
，曲線
：
.以極點為坐標原點，極軸為
軸正半軸建立直角坐標系
，曲線
的參數方程為
（
為參數）.
（1）求，的直角坐標方程；
（2）與，交于不同四點，這四點在上的排列順次為
，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在海島A上有一座海拔1千米的山，山頂設有一個觀察站P，上午11時，測得一輪船在島北偏東30°，俯角為30°的B處，到11時10分又測得該船在島北偏西60°，俯角為60°的C處．
(1)求船的航行速度是每小時多少千米？
(2)又經過一段時間后，船到達海島的正西方向的D處，問此時船距島A有多遠？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，O為坐標原點，點F為拋物線C1：
的焦點，且拋物線C1上點P處的切線與圓C2：
相切于點Q．
（Ⅰ）當直線PQ的方程為
時，求 拋物線C1的方程；
（Ⅱ）當正數P變化時，記S1 ，S2分別為△FPQ，△FOQ的面積，求
的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的前
項和為
，且
，
（1）求證：數列
為等比數列，并求出數列的通項公式；
（2）是否存在實數
，對任意
，不等式
恒成立？若存在，求出的取值范圍，若不存在請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設有三個鄉鎮，分別位于一個矩形
的兩個頂點M，N及
的中點S處，
，現要在該矩形的區域內（含邊界），且與M，N等距離的一點O處設一個宣講站，記O點到三個鄉鎮的距離之和為
．
（1）設
，試將L表示為x的函數并寫出其定義域；
（2）試利用（1）的函數關系式確定宣講站O的位置，使宣講站O到三個鄉鎮的距離之和最小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
的離心率為2，過點
、斜率為1的直線
與雙曲線
交于
、
兩點且
，
.
（1）求雙曲線方程。
（2）設
為雙曲線右支上動點，
為雙曲線的右焦點，在
軸負半軸上是否存在定點
，使得
？若存在，求出點的坐標；若不存在，請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
