【題目】以下命題正確的是（ ）
A. 若直線
，
，
，則直線a，b異面
B. 空間內任意三點可以確定一個平面
C. 空間四點共面，則其中必有三點共線
D. 直線，
，
，則直線a，b異面
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】“既要金山銀山，又要綠水青山”。某風景區在一個直徑
為
米的半圓形花圓中設計一條觀光線路。打算在半圓弧上任選一點
（與
不重合），沿
修一條直線段小路，在路的兩側（注意是兩側）種植綠化帶；再沿弧
修一條弧形小路，在小路的一側（注意是一側）種植綠化帶，小路與綠化帶的寬度忽略不計。
（1）設
（弧度），將綠化帶的總長度表示為
的函數
；
（2）求綠化帶的總長度的最大值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】由四個不同的數字
1，2，4，
組成無重復數字的三位數.（最后的結果用數字表達）
（Ⅰ）若
,其中能被5整除的共有多少個？
（Ⅱ）若
，其中能被3整除的共有多少個？
（Ⅲ）若
，其中的偶數共有多少個？
（Ⅳ）若所有這些三位數的各位數字之和是252，求．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2015年12月10日，我國科學家屠呦呦教授由于在發現青蒿素和治療瘧疾的療法上的貢獻獲得諾貝爾醫學獎，以青蒿素類藥物為主的聯合療法已經成為世界衛生組織推薦的抗瘧疾標準療法，目前，國內青蒿人工種植發展迅速，調查表明，人工種植的青蒿的長勢與海撥高度、土壤酸堿度、空氣濕度的指標有極強的相關性，現將這三項的指標分別記為
，并對它們進行量化：0表示不合格，1表示臨界合格，2表示合格，再用綜合指標
的值評定人工種植的青蒿的長勢等級，若
，則長勢為一級；若
，則長勢為二極；若
，則長勢為三級，為了了解目前人工種植的青蒿的長勢情況，研究人員隨機抽取了10塊青蒿人工種植地，得到如下結果：
種植地編號 |
|
|
|
|
|
|
|
|
|
|
|
種植地編號 |
|
|
|
|
|
|
|
|
|
|
|
（1）若該地有青蒿人工種植地180個，試估計該地中長勢等級為三級的個數；
（2）從長勢等級為一級的青蒿人工種植地中隨機抽取兩個，求這兩個人工種植地的綜合指標
均為4個概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在“新零售”模式的背景下，某大型零售公司為推廣線下分店，計劃在S市的A區開設分店．為了確定在該區開設分店的個數，該公司對該市已開設分店的其他區的數據作了初步處理后得到下列表格．記x表示在各區開設分店的個數，y表示這x個分店的年收入之和．
x（個） | 2 | 3 | 4 | 5 | 6 |
y（百萬元） | 2.5 | 3 | 4 | 4.5 | 6 |
(1)該公司經過初步判斷，可用線性回歸模型擬合y與x的關系，求y關于x的線性回歸方程；
（2）假設該公司在A區獲得的總年利潤z（單位：百萬元）與x，y之間滿足的關系式為：
,請結合（1）中的線性回歸方程，估算該公司應在A區開設多少個分店，才能使A區平均每個分店的年利潤最大？
附：回歸方程
中的斜率和截距的最小二乘估計公式分別為：
，
.
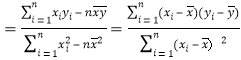（參考數據：
，
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一半徑為
米的水輪如圖所示，水輪圓心
距離水面
米；已知水輪按逆時針做勻速轉動，每
秒轉一圈，如果當水輪上點
從水中浮現時（圖中點
）開始計算時間.
（1）以水輪所在平面與水面的交線為
軸，以過點且與水面垂直的直線為
軸，建立如圖所示的直角坐標系，試將點距離水面的高度
（單位：米）表示為時間
（單位：秒）的函數；
（2）在水輪轉動的任意一圈內，有多長時間點距水面的高度超過米？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
(0<φ<π，ω>0)為偶函數，且函數y＝f(x)圖象的兩相鄰對稱軸間的距離為
.若將函數y＝f(x)的圖象向右平移
個單位后，再將得到的圖象上各點的橫坐標伸長到原來的4倍，縱坐標不變，得到函數y＝g(x)的圖象，則g(x)在下列區間上是減函數的是( )
A. 
B. [0，π]
C. [2π，3π] D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
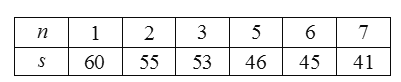
【題目】某農科所發現，一種作物的年收獲量
（單位：
）與它“相近”作物的株數
具有相關關系（所謂兩株作物“相近”是指它們的直線距離不超過
），并分別記錄了相近作物的株數為
時，該作物的年收獲量的相關數據如下：
（1）根據研究發現，該作物的年收獲量可能和它“相近”作物的株數有以下兩種回歸方程：
，利用統計知識，結合相關系數
比較使用哪種回歸方程更合適；
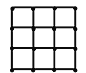
（2）農科所在如下圖所示的正方形地塊的每個格點（指縱、橫直線的交叉點）處都種了一株該作物，其中每個小正方形的面積為
，若在所種作物中隨機選取一株，求它的年收獲量的分布列與數學期望.（注：年收獲量以（1）中選擇的回歸方程計算所得數據為依據）
參考公式：線性回歸方程為
，其中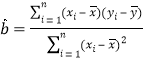
，
，
相關系數
；
參考數值：
，
，
，其中
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
