
【題目】在直角坐標系xOy中,曲線C1的參數方程為![]() (
(![]() 為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為
為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為![]() .
.
(1)寫出曲線C1和C2的直角坐標方程;
(2)已知P為曲線C2上的動點,過點P作曲線C1的切線,切點為A,求|PA|的最大值.
【答案】(1)C1的直角坐標方程為![]() ;C2的直角坐標方程為
;C2的直角坐標方程為![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() (
(![]() 為參數),消去參數
為參數),消去參數![]() ,可得曲線C1的直角坐標方程.由
,可得曲線C1的直角坐標方程.由![]() ,得ρ2+3ρ2sin2θ=4,結合極坐標與直角坐標的互化公式可得曲線C2的直角坐標方程;
,得ρ2+3ρ2sin2θ=4,結合極坐標與直角坐標的互化公式可得曲線C2的直角坐標方程;
(2)由P為曲線C2上的動點,設P(2cosα,sinα),則P與圓的圓心的距離![]() ,利用二次函數求最值,再由勾股定理求|PA|的最大值.
,利用二次函數求最值,再由勾股定理求|PA|的最大值.
解:(1)由![]() (
(![]() 為參數),消去參數
為參數),消去參數![]() ,可得
,可得![]() .
.
∴曲線C1的直角坐標方程為![]() ;
;
由![]() ,得ρ2+3ρ2sin2θ=4,
,得ρ2+3ρ2sin2θ=4,
即x2+y2+3y2=4,即![]() .
.
∴曲線C2的直角坐標方程為![]() ;
;
(2)∵P為曲線C2上的動點,又曲線C2的參數方程為![]()
∴設P(2cosα,sinα),
則P與圓C1的圓心的距離
 .
.
要使|PA|的最大值,則d最大,當sinα![]() 時,d有最大值為
時,d有最大值為![]() .
.
∴|PA|的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】2020年是我國垃圾分類逐步凸顯效果關鍵的一年.在國家高度重視,重拳出擊的前提下,高強度、高頻率的宣傳教育能有效縮短我國生活垃圾分類走入世界前列所需的時間,打好垃圾分類這場“持久戰”,“全民戰”.某市做了一項調查,在一所城市中學和一所縣城中學隨機各抽取15名學生,對垃圾分類知識進行問答,滿分為100分,他們所得成績如下:
城市中學學生成績分別為:73 71 83 86 92 70 88 93 73 97 87 88 74 86 85
縣城中學學生成績分別為:60 64 71 91 60 76 72 85 81 72 62 74 73 63 72

(1)根據上述兩組數據在圖中完成兩所中學學生成績的莖葉圖,并通過莖葉圖比較兩所中學學生成績的平均分及分散程度;(不要求計算出具體值,給出結論即可)
(2)記這30名學生成績80分以上為良好,80分以下為一般,完善表格,并判斷是否有99%的把握認為該城市中學和縣城中學的學生在了解垃圾分類知識上有差異?(結果保留三位小數)
學生成績 | 良好 | 一般 | 合計 |
城市中學學生 | |||
縣城中學學生 | |||
合計 |
附: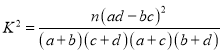 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】菱形![]() 中,
中,![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
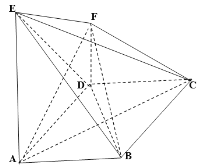
(1)證明:直線![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)線段![]() 上是否存在點
上是否存在點![]() 使得直線
使得直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ?若存在,求
?若存在,求![]() ;若不存在,說明理由.
;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左頂點為
的左頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,離心率為
,離心率為![]() ,
,![]() 是橢圓上的一個動點(不與左、右頂點重合),且
是橢圓上的一個動點(不與左、右頂點重合),且![]() 的周長為6,點
的周長為6,點![]() 關于原點的對稱點為
關于原點的對稱點為![]() ,直線
,直線![]() 交于點
交于點![]() .
.
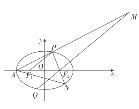
(1)求橢圓方程;
(2)若直線![]() 與橢圓交于另一點
與橢圓交于另一點![]() ,且
,且![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過雙曲線C:![]() 1(a>0,b>0)右焦點F2作雙曲線一條漸近線的垂線,垂足為P,與雙曲線交于點A,若
1(a>0,b>0)右焦點F2作雙曲線一條漸近線的垂線,垂足為P,與雙曲線交于點A,若![]() ,則雙曲線C的漸近線方程為( )
,則雙曲線C的漸近線方程為( )
A.y=±![]() xB.y=±xC.y=±2xD.y=±
xB.y=±xC.y=±2xD.y=±![]() x
x
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐![]() 中,
中,![]() 與
與![]() 均為等腰直角三角形,且
均為等腰直角三角形,且![]() ,
,![]() ,
,![]() 為
為![]() 上一點,且
上一點,且![]() 平面
平面![]() .
.
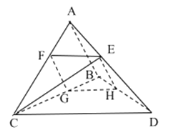
(1)求證:![]() ;
;
(2)過![]() 作一平面分別交
作一平面分別交![]() ,
, ![]() ,
, ![]() 于
于![]() ,
,![]() ,
,![]() ,若四邊形
,若四邊形![]() 為平行四邊形,求多面體
為平行四邊形,求多面體![]() 的表面積.
的表面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com