
【題目】菱形![]() 中,
中,![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
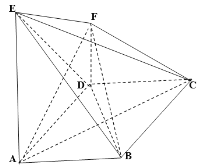
(1)證明:直線![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)線段![]() 上是否存在點
上是否存在點![]() 使得直線
使得直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ?若存在,求
?若存在,求![]() ;若不存在,說明理由.
;若不存在,說明理由.
【答案】(1)證明見解析(2)![]() (3)存在,
(3)存在,![]()
【解析】
(1)建立以![]() 為原點,分別以
為原點,分別以![]() ,
,![]() (
(![]() 為
為![]() 中點),
中點),![]() 的方向為
的方向為![]() 軸,
軸,![]() 軸,
軸,![]() 軸正方向的空間直角坐標系,求出直線
軸正方向的空間直角坐標系,求出直線![]() 的方向向量,平面
的方向向量,平面![]() 的法向量,證明向量垂直,得到線面平行;
的法向量,證明向量垂直,得到線面平行;
(2)利用空間向量法求出二面角的余弦值,再由同角三角函數的基本關系求出正弦值;
(3)設![]() ,則
,則![]() ,利用空間向量求表示出線面角的正弦值,求出
,利用空間向量求表示出線面角的正弦值,求出![]() 的值,得解.
的值,得解.
解:建立以![]() 為原點,分別以
為原點,分別以![]() ,
,![]() (
(![]() 為
為![]() 中點),
中點),![]() 的方向為
的方向為![]() 軸,
軸,![]() 軸,
軸,![]() 軸正方向的空間直角坐標系(如圖),
軸正方向的空間直角坐標系(如圖),
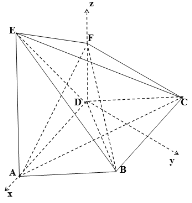
則![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
(1)證明:![]() ,
,![]() ,
,
設![]() 為平面
為平面![]() 的法向量,
的法向量,
則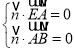 ,即
,即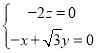 ,
,
可得![]() ,
,
又![]() ,可得
,可得![]() ,
,
又因為直線![]() 平面
平面![]() ,所以直線
,所以直線![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() ,
,![]() ,
,
設![]() 為平面
為平面![]() 的法向量,
的法向量,
則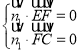 ,即
,即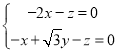 ,可得
,可得![]() ,
,
設![]() 為平面
為平面![]() 的法向量,
的法向量,
則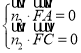 ,即
,即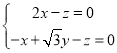 ,可得
,可得![]() ,
,
所以 ,
,
![]()
所以二面角![]() 的正弦值為
的正弦值為![]() ;
;
(3)設![]() ,則
,則![]() ,
,
則![]() ,
,![]() ,
,
設![]() 為平面
為平面![]() 的法向量,
的法向量,
則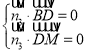 ,即
,即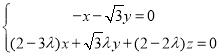 ,
,
可得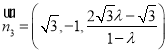 ,
,
由![]() ,得
,得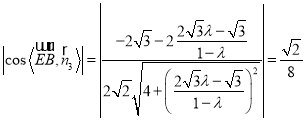 ,
,
解得![]() 或
或![]() (舍),所以
(舍),所以![]() .
.


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:高中數學 來源: 題型:
【題目】已知![]() 為拋物線
為拋物線![]() 上的一點,
上的一點,![]() ,
,![]() 為拋物線上異于點
為拋物線上異于點![]() 的兩點,且直線
的兩點,且直線![]() 的斜率與直線
的斜率與直線![]() 的斜率互為相反數.
的斜率互為相反數.
(1)求直線![]() 的斜率;
的斜率;
(2)設直線![]() 過點
過點![]() 并交拋物線于
并交拋物線于![]() ,
,![]() 兩點,且
兩點,且![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,試探究
,試探究![]() 與
與![]() 的夾角是否為定值,若是則求出定值,若不是,說明理由.
的夾角是否為定值,若是則求出定值,若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020元旦聯歡晚會上,![]() ,
,![]() 兩班各設計了一個摸球表演節目的游戲:
兩班各設計了一個摸球表演節目的游戲:![]() 班在一個紙盒中裝有1個紅球,1個黃球,1個白球,這些球除顏色外完全相同,記事件
班在一個紙盒中裝有1個紅球,1個黃球,1個白球,這些球除顏色外完全相同,記事件![]() :同學們有放回地每次摸出1個球,重復
:同學們有放回地每次摸出1個球,重復![]() 次,
次,![]() 次摸球中既有紅球,也有黃球,還有白球;
次摸球中既有紅球,也有黃球,還有白球;![]() 班在一個紙盒中裝有1個藍球,1個黑球,這些球除顏色外完全相同,記事件
班在一個紙盒中裝有1個藍球,1個黑球,這些球除顏色外完全相同,記事件![]() :同學們有放回地每次摸出1個球,重復
:同學們有放回地每次摸出1個球,重復![]() 次,
次,![]() 次摸球中既有藍球,也有黑球,事件
次摸球中既有藍球,也有黑球,事件![]() 發生的概率為
發生的概率為![]() ,事件
,事件![]() 發生的概率為
發生的概率為![]() .
.
(1)求概率![]() ,
,![]() 及
及![]() ,
,![]() ;
;
(2)已知![]() ,其中
,其中![]() ,
,![]() 為常數,求
為常數,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是以
是以![]() 為直徑的圓上一點,
為直徑的圓上一點,![]() ,等腰梯形
,等腰梯形![]() 所在的平面垂直于⊙
所在的平面垂直于⊙![]() 所在的平面,且
所在的平面,且![]() .
.
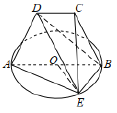
(1)求![]() 與
與![]() 所成的角;
所成的角;
(2)若異面直線![]() 和
和![]() 所成的角為
所成的角為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 為矩形,
為矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.
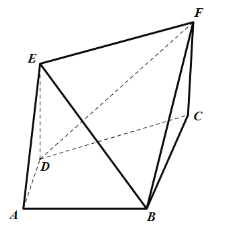
(1)求證:![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點P,使得直線
上是否存在點P,使得直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,若存在,求出線段
,若存在,求出線段![]() 的長,若不存在,請說明理由.
的長,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】今年,新型冠狀病毒來勢兇猛,老百姓一時間“談毒色變”,近來,有關喝白酒可以預防病毒的說法一直在民間流傳,更有人拿出“醫”字的繁體字“醫”進行解讀為:醫治瘟疫要喝酒,為了調查喝白酒是否有助于預防病毒,我們調查了1000人的喝酒生活習慣與最終是否得病進行了統計,表格如下:
每周喝酒量(兩) |
|
|
|
|
|
人數 | 100 | 300 | 450 | 100 |
|
規定:①每周喝酒量達到4兩的叫常喝酒人,反之叫不常喝酒人;
②每周喝酒量達到8兩的叫有酒癮的人.
(1)求![]() 值,從每周喝酒量達到6兩的人中按照分層抽樣選出6人,再從這6人中選出2人,求這2人中無有酒癮的人的概率;
值,從每周喝酒量達到6兩的人中按照分層抽樣選出6人,再從這6人中選出2人,求這2人中無有酒癮的人的概率;
(2)請通過上述表格中的統計數據,填寫完下面的![]() 列聯表,并通過計算判斷是否能在犯錯誤的概率不超過0.1的前提下認為是否得病與是否常喝酒有關?并對民間流傳的說法做出你的判斷.
列聯表,并通過計算判斷是否能在犯錯誤的概率不超過0.1的前提下認為是否得病與是否常喝酒有關?并對民間流傳的說法做出你的判斷.
常喝酒 | 不常喝酒 | 合計 | |
得病 | |||
不得病 | 250 | 650 | |
合計 |
參考公式: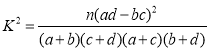 ,其中
,其中![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系![]() 中,
中,
曲線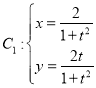 (
(![]() 為參數),
為參數),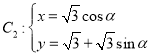 (
(![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() (
(![]() 且
且![]() ).
).
(1)求![]() 與
與![]() 的極坐標方程;
的極坐標方程;
(2)若![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() ,當
,當![]() 為何值時,
為何值時,![]() 最大,并求最大值.
最大,并求最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1的參數方程為![]() (
(![]() 為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為
為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為![]() .
.
(1)寫出曲線C1和C2的直角坐標方程;
(2)已知P為曲線C2上的動點,過點P作曲線C1的切線,切點為A,求|PA|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
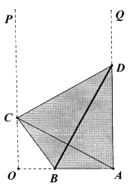
【題目】在國家批復成立江北新區后,南京市政府規劃在新區內的一條形地塊上新建一個全民健身中心,規劃區域為四邊形ABCD,如圖![]() ,
,![]() ,點B在線段OA上,點C、D分別在射線OP與AQ上,且A和C關于BD對稱.已知
,點B在線段OA上,點C、D分別在射線OP與AQ上,且A和C關于BD對稱.已知![]() .
.
(1)若![]() ,求BD的長;
,求BD的長;
(2)問點C在何處時,規劃區域的面積最小?最小值是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com