
【題目】如圖,四棱錐P﹣ABCD中,底面ABCD為平行四邊形,PA⊥底面ABCD,M是棱PD的中點,且PA=AB=AC=2,BC=2 ![]() .
. 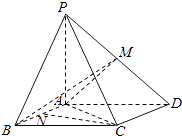
(1)求證:CD⊥平面PAC;
(2)如果如果N是棱AB上一點,且直線CN與平面MAB所成角的正弦值為 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)證明:連結AC.因為在△ABC中,AB=AC=2, ![]() ,
,
所以AB2+AC2=BC2,所以AB⊥AC.
因為AB∥CD,所以AC⊥CD.
又因為PA⊥底面ABCD,所以PA⊥CD.
因為AC∩PA=A,
所以CD⊥平面PAC.
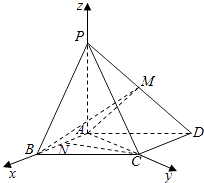
(2)解:如圖,以A為原點,AB,AC,AP所在直線分別為x,y,z軸,建立空間直角坐標系.
則A(0,0,0),P(0,0,2),B(2,0,0),C(0,2,0),D(﹣2,2,0),因為M是棱PD的中點,所以M(﹣1,1,1).
所以 ![]() ,
,
設 ![]() =(x,y,z)為平面MAB的法向量,
=(x,y,z)為平面MAB的法向量,
則 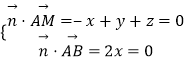 ,
,
令y=1,得平面MAB的法向量 ![]() =(0,1,﹣1),
=(0,1,﹣1),
因為N是在棱AB上一點,所以設N(x,0,0), ![]() =(﹣x,2,0).
=(﹣x,2,0).
因為直線CN與平面MAB所成角的正弦值為 ![]() ,
,
設直線CN與平面MAB所成角為α,
則sinα=|cos< ![]() >|=
>|= 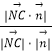 =
= ![]() =
= ![]() ,
,
解得x=1,即AN=1,NB=1,所以 ![]() =1.
=1.
【解析】(1)連結AC,由勾股定理得AB⊥AC,從而AC⊥CD,由線面垂直得PA⊥CD,由此能證明CD⊥平面PAC.(2)以A為原點,AB,AC,AP所在直線分別為x,y,z軸,建立空間直角坐標系,由直線CN與平面MAB所成角的正弦值為 ![]() ,利用向量法能求出
,利用向量法能求出 ![]() 的值.
的值.
【考點精析】根據題目的已知條件,利用直線與平面垂直的判定和空間角的異面直線所成的角的相關知識可以得到問題的答案,需要掌握一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想;已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則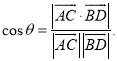 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某市政府為了確定一個較為合理的居民用電標準,必須先了解全市居民日常用電量的分布情況.現采用抽樣調查的方式,獲得了n位居民在2012年的月均用電量(單位:度)數據,樣本統計結果如下圖表:
分 組 | 頻 數 | 頻 率 |
[0,10) | 0.05 | |
[10,20) | 0.10 | |
[20,30) | 30 | |
[30,40) | 0.25 | |
[40,50) | 0.15 | |
[50,60] | 15 | |
合 計 | n | 1 |
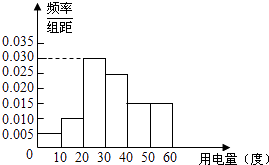
(1)求月均用電量的中位數與平均數估計值;
(2)如果用分層抽樣的方法從這n位居民中抽取8位居民,再從這8位居民中選2位居民,那么至少有1位居民月均用電量在30至40度的概率是多少?
(3)用樣本估計總體,把頻率視為概率,從這個城市隨機抽取3位居民(看作有放回的抽樣),求月均用電量在30至40度的居民數X的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給n個自上而下相連的正方形著黑色或白色.當n≤4時,在所有不同的著色方案中,黑色正方形互不相鄰的著色方案如圖所示,由此推斷,當n=6時,至少有兩個黑色正方形相鄰的著色方案共有( )種. 
A.21
B.32
C.43
D.54
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題中
① 非零向量![]() 滿足
滿足![]() ,則
,則![]() 的夾角為
的夾角為![]() ;
;
② ![]()
![]() >0是
>0是![]() 的夾角為銳角的充要條件;
的夾角為銳角的充要條件;
③若![]() 則
則![]() 必定是直角三角形;
必定是直角三角形;
④△ABC的外接圓的圓心為O,半徑為1,若![]() ,且
,且![]() ,則向量
,則向量![]() 在向量
在向量![]() 方向上的投影為
方向上的投影為![]() .
.
以上命題正確的是 __________ (注:把你認為正確的命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a∈R,函數f(x)=xln(﹣x)+(a﹣1)x.
(1)若f(x)在x=﹣e處取得極值,求函數f(x)的單調區間;
(2)求函數f(x)在區間[﹣e2 , ﹣e﹣1]上的最大值g(a).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com