
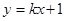 與圓
與圓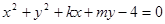 交于M,N兩點,且M,N關于直線
交于M,N兩點,且M,N關于直線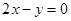 對稱,動點P(a,b)在不等式組
對稱,動點P(a,b)在不等式組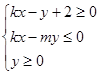 表示的平面區域內部及邊界上運動,則
表示的平面區域內部及邊界上運動,則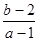 取值范圍是( )
取值范圍是( )A. | B. | C. | D.   |
 ,
,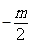 ),且直線2x-y=0與直線y=kx+1垂直.
),且直線2x-y=0與直線y=kx+1垂直. ,m=-1.
,m=-1.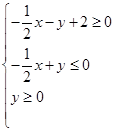

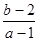 表示可行域內點Q和點P(1,2)連線的斜率,
表示可行域內點Q和點P(1,2)連線的斜率,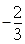 ,
, ∪[2,+∞)
∪[2,+∞) ∪[2,+∞).
∪[2,+∞).

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com