
(1)求函數f(x)的單調區間;
(2)當x∈[![]() -1,e-1]時,不等式f(x)<m恒成立,求實數m的取值范圍;
-1,e-1]時,不等式f(x)<m恒成立,求實數m的取值范圍;
(3)關于x的方程f(x)=x2+x+a在[0,2]上恰有兩個相異實根,求實數a的取值范圍.(e為自然常數,約等于2.718 281 828 459)
解:(1)函數定義域為(-∞,-1)∪(-1,+∞),∵f′(x)=2[(x+1)![]() ]=
]=![]() ,
,
由f′(x)>0,得-2<x<-1或x>0;由f′(x)<0,得x<-2或-1<x<0,
則遞增區間是(-2,-1),(0,+∞),遞減區間是(-∞,-2),(-1,0).
(2)由f′(x)=![]() =0,得x=0或x=-2.
=0,得x=0或x=-2.
由(1)知,f(x)在[![]() -1,0]上遞減,在[0,e-1]上遞增.
-1,0]上遞減,在[0,e-1]上遞增.
又f(![]() -1)=
-1)=![]() +2,f(e-1)=e2-2,且e2-2>
+2,f(e-1)=e2-2,且e2-2>![]() +2,∴x∈[
+2,∴x∈[![]() -1,e-1]時,[f(x)]max=e2-2,
-1,e-1]時,[f(x)]max=e2-2,
故m>e2-2時,不等式f(x)<m恒成立.
(3)方程f(x)=x2+x+a,即x-a+1-ln(1+x)2=0.記g(x)=x-a+1-ln(1+x)2,
則g′(x)=1![]() =
=![]() .由g′(x)>0,得x<-1或x>1,由g′(x)<0,得-1<x<1.
.由g′(x)>0,得x<-1或x>1,由g′(x)<0,得-1<x<1.
∴g(x)在[0,1]上遞減,在[1,2]上遞增.
為使f(x)=x2+x+a在[0,2]上恰好有兩個相異的實根,只需g(x)=0在[0,1)和(1,2]上各有一個實根,于是有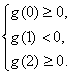 解得2-2ln2<a≤3-2ln3.
解得2-2ln2<a≤3-2ln3.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
|
| (a+b)-(a-b)f(a-b) |
| 2 |
| A、a | B、b |
| C、a,b中較小的數 | D、a,b中較大的數 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1-x |
| 1+x |
A、-
| ||
B、-
| ||
| C、-1 | ||
| D、-2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| A、a<0 | B、0≤a<1 |
| C、a=1 | D、a>1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com