
 中,角
中,角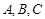 所對的邊分別為
所對的邊分別為 ,若
,若 。
。 ;
; 的平分線交
的平分線交 于
于 ,且
,且 ,求
,求 的值。
的值。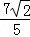 .
. 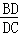 =
=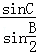 ,由第一問知道C=B,
,由第一問知道C=B,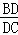 ="2cos"
="2cos" 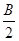 . 8分
. 8分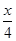 =45°.--9分
=45°.--9分 ,∴
,∴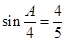 ,
,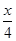 )=cos45°cos
)=cos45°cos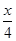 +sin45°sin
+sin45°sin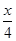 =
=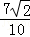 .
.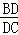 =2cos
=2cos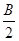 =2cosα=
=2cosα=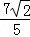 . 12分
. 12分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com