
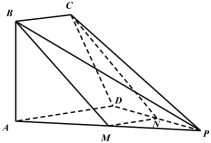
【題目】如圖,四棱錐![]() 的底面為直角梯形,
的底面為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.

(Ⅰ)求證:![]() 平面
平面![]()
(Ⅱ)若平面![]() 平面
平面![]() ,異面直線
,異面直線![]() 與
與![]() 所成角為60°,且
所成角為60°,且![]() 是鈍角三角形,求二面角
是鈍角三角形,求二面角![]() 的正弦值
的正弦值
【答案】(Ⅰ)詳見解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取![]() 的中點
的中點![]() ,連接
,連接![]() ,證明四邊形
,證明四邊形![]() 為平行四邊形,得到
為平行四邊形,得到![]() 即可
即可
(Ⅱ)由條件得出![]() ,然后證明
,然后證明![]() 平面
平面![]() ,然后以
,然后以![]() 為坐標原點,
為坐標原點,![]() 所在直線為
所在直線為![]() 軸、
軸、![]() 軸建立空間直角坐標系,分別求出平面
軸建立空間直角坐標系,分別求出平面![]() 和平面
和平面![]() 的法向量即可.
的法向量即可.
(Ⅰ)證明:取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,
因為![]() 為
為![]() 的中點,則
的中點,則![]() ,且
,且![]() ,
,
又![]() ,且
,且![]() ,所以
,所以![]() ,
,![]() ,
,
所以四邊形![]() 為平行四邊形,
為平行四邊形,
所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
(Ⅱ)由題意可知![]() ,所以
,所以![]() 或其補角為異面直線
或其補角為異面直線![]() 與
與![]() 所成角,
所成角,
又![]() ,
,![]() 為鈍角三角形,所以
為鈍角三角形,所以![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
以![]() 為坐標原點,
為坐標原點,![]() 所在直線為
所在直線為![]() 軸、
軸、![]() 軸建立空間直角坐標系,
軸建立空間直角坐標系,
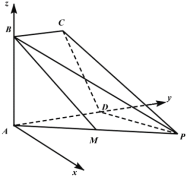
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
向量![]() ,
,![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]()
由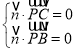 得
得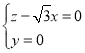 ,令
,令![]() ,
,
得平面![]() 的一個法向量為
的一個法向量為![]() ,
,
同理可得平面![]() 的一個法向量為
的一個法向量為![]()
設(shè)二面角![]() 的平面角為
的平面角為![]() ,
,
則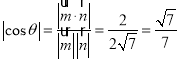
則![]()
故二面角![]() 的正弦值為
的正弦值為![]()


科目:高中數(shù)學 來源: 題型:
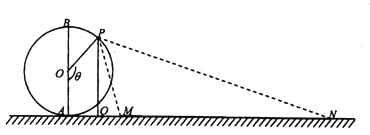
【題目】如圖,摩天輪的半徑![]() 為
為![]() ,它的最低點
,它的最低點![]() 距地面的高度忽略不計.地上有一長度為
距地面的高度忽略不計.地上有一長度為![]() 的景觀帶
的景觀帶![]() ,它與摩天輪在同一豎直平面內(nèi),且
,它與摩天輪在同一豎直平面內(nèi),且![]() .點
.點![]() 從最低點
從最低點![]() 處逆時針方向轉(zhuǎn)動到最高點
處逆時針方向轉(zhuǎn)動到最高點![]() 處,記
處,記![]() .
.
(1)當![]() 時,求點
時,求點![]() 距地面的高度
距地面的高度![]() ;
;
(2)試確定![]() 的值,使得
的值,使得![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 的最大值為
的最大值為![]() ,且曲線
,且曲線![]() 在x=0處的切線與直線
在x=0處的切線與直線![]() 平行(其中e為自然對數(shù)的底數(shù)).
平行(其中e為自然對數(shù)的底數(shù)).
(1)求實數(shù)a,b的值;
(2)如果![]() ,且
,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 在
在![]() 上存在單調(diào)遞增區(qū)間,求實數(shù)
上存在單調(diào)遞增區(qū)間,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)設(shè)![]() ,若
,若![]() ,恒有
,恒有![]() 成立,求
成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】東京夏季奧運會推遲至2021年7月23日至8月8日舉行,此次奧運會將設(shè)置4![]() 100米男女混泳接力賽這一新的比賽項目,比賽的規(guī)則是:每個參賽國家派出2男2女共計4名運動員參加比賽,按照仰泳
100米男女混泳接力賽這一新的比賽項目,比賽的規(guī)則是:每個參賽國家派出2男2女共計4名運動員參加比賽,按照仰泳![]() 蛙泳
蛙泳![]() 蝶泳
蝶泳![]() 自由泳的接力順序,每種泳姿100米且由1名運動員完成,且每名運動員都要出場.若中國隊確定了備戰(zhàn)該項目的4名運動員名單,其中女運動員甲只能承擔仰泳或者自由泳,男運動員乙只能承擔蝶泳或者蛙泳,剩下2名運動員四種泳姿都可以承擔,則中國隊參賽的安排共有( )
自由泳的接力順序,每種泳姿100米且由1名運動員完成,且每名運動員都要出場.若中國隊確定了備戰(zhàn)該項目的4名運動員名單,其中女運動員甲只能承擔仰泳或者自由泳,男運動員乙只能承擔蝶泳或者蛙泳,剩下2名運動員四種泳姿都可以承擔,則中國隊參賽的安排共有( )
A.144種B.8種C.24種D.12種
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)X是有限集,t為正整數(shù),F是包含t個子集的子集族:F=![]() .如果F中的部分子集構(gòu)成的集族S滿足:對S中任意兩個不相等的集合A、B,
.如果F中的部分子集構(gòu)成的集族S滿足:對S中任意兩個不相等的集合A、B,![]() 均不成立,則稱S為反鏈.設(shè)S1為包含集合最多的反鏈,S2是任意反鏈.證明:存在S2到S1的單射f,滿足
均不成立,則稱S為反鏈.設(shè)S1為包含集合最多的反鏈,S2是任意反鏈.證明:存在S2到S1的單射f,滿足![]() 或
或![]() 成立.
成立.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
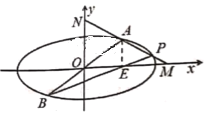
【題目】如圖,已知橢圓C:![]() 過原點的直線與橢圓交于A,B兩點(點A在第一象限),過點A作x軸的垂線,垂足為點
過原點的直線與橢圓交于A,B兩點(點A在第一象限),過點A作x軸的垂線,垂足為點![]() ,設(shè)直線BE與橢圓的另一交點為P,連接AP得到直線l,交x軸于點M,交y軸于點N.
,設(shè)直線BE與橢圓的另一交點為P,連接AP得到直線l,交x軸于點M,交y軸于點N.
(1)若![]() ,求直線AP的斜率;
,求直線AP的斜率;
(2)記![]() 的面積分別為S1,S2,S3,求
的面積分別為S1,S2,S3,求![]() 的的最大值.
的的最大值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com