
已知曲線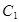 上任意一點
上任意一點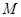 到直線
到直線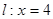 的距離是它到點
的距離是它到點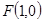 距離的
距離的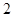 倍;曲線
倍;曲線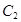 是以原點為頂點,
是以原點為頂點,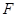 為焦點的拋物線.
為焦點的拋物線.
(Ⅰ)求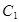 ,
,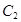 的方程;
的方程;
(Ⅱ)過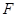 作兩條互相垂直的直線
作兩條互相垂直的直線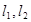 ,其中
,其中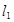 與
與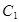 相交于點
相交于點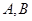 ,
,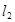 與
與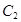 相交于點
相交于點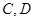 ,求四邊形
,求四邊形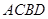 面積的取值范圍.
面積的取值范圍.
(Ⅰ)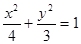 ,
,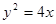 ;(Ⅱ)
;(Ⅱ)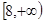 .
.
【解析】
試題分析:(Ⅰ)求 曲線 ,則設該曲線上某點
,則設該曲線上某點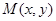 ,然后根據題目條件,得到關于
,然后根據題目條件,得到關于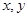 的方程,再化簡即可得到
的方程,再化簡即可得到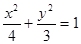 .曲線
.曲線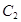 可以根據拋物線的幾何性質得到,
可以根據拋物線的幾何性質得到,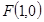 為拋物線焦點,從而得到
為拋物線焦點,從而得到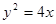 ;(Ⅱ)用點斜式設出
;(Ⅱ)用點斜式設出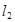 的方程為
的方程為 ,與拋物線方程聯(lián)立,即可得到關于點
,與拋物線方程聯(lián)立,即可得到關于點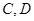 坐標的方程.再根據韋達定理即得到
坐標的方程.再根據韋達定理即得到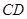 的長度.由題意可設
的長度.由題意可設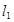 的方程為
的方程為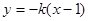 ,代入
,代入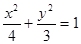 可得關于點
可得關于點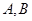 坐標的方程.再根據韋達定理即得到
坐標的方程.再根據韋達定理即得到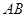 的長度.因為
的長度.因為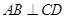 ,從而四邊形
,從而四邊形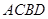 的面積為
的面積為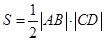 ,經化簡,通過基本不等式即可得到四邊形
,經化簡,通過基本不等式即可得到四邊形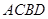 面積的取值范圍為
面積的取值范圍為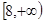 .
.
試題解析:(Ⅰ)設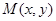 ,則由題意有
,則由題意有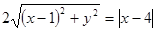 ,化簡得:
,化簡得: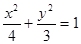 .
.
故 的方程為
的方程為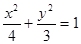 ,易知
,易知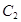 的方程為
的方程為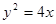 .
4分
.
4分
(Ⅱ)由題意可設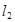 的方程為
的方程為 ,代入
,代入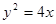 得
得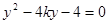 ,
,
設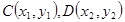 ,則
,則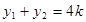 ,
,
所以 .
7分
.
7分
因為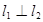 ,故可設
,故可設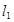 的方程為
的方程為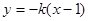 ,代入
,代入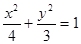 得
得
 ,設
,設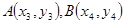 ,則
,則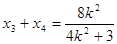 ,
,
所以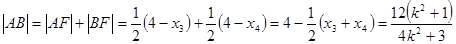 . 10分
. 10分
故四邊形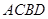 的面積為
的面積為

(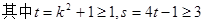 )
)
設 ,因此
,因此
 ,當且僅當
,當且僅當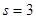 即
即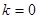 等號成立.
等號成立.
故四邊形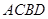 面積的取值范圍為
面積的取值范圍為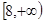 .
13分
.
13分
考點:1.曲線與方程;2.拋物線的幾何性質;3.直線與圓錐曲線的位置關系;4.基本不等式;5.函數的單調性.


科目:高中數學 來源:2014屆河南省許昌市五校高二下學期第一次聯(lián)考文科數學試卷(解析版) 題型:解答題
已知曲線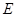 上任意一點
上任意一點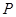 到兩個定點
到兩個定點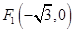 ,
,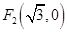 的距離之和為4.
的距離之和為4.
(1)求曲線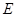 的方程;
的方程;
(2)設過(0,-2)的直線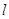 與曲線
與曲線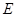 交于
交于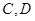 兩點,且
兩點,且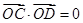 (
(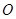 為原點),求直線
為原點),求直線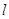 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省廣州市高三數學解析幾何專題試卷 題型:解答題
已知曲線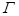 上任意一點
上任意一點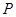 到兩個定點
到兩個定點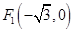 和
和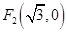 的距離之和為4.
的距離之和為4.
(1)求曲線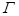 的方程;
的方程;
(2)設過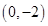 的直線
的直線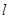 與曲線
與曲線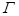 交于
交于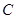 、
、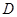 兩點,且
兩點,且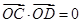 (
(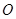 為坐標原點),求直線
為坐標原點),求直線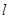 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年內蒙古巴彥淖爾市高三上學期期末考試文科數學試卷 題型:解答題
已知曲線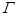 上任意一點
上任意一點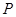 到兩個定點
到兩個定點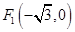 和
和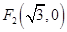 的距離之和為4.
的距離之和為4.
(1)求曲線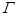 的方程;
的方程;
(2)設過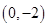 的直線
的直線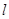 與曲線
與曲線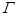 交于
交于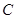 、
、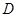 兩點,且
兩點,且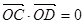 (
(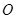 為坐標原點),求直線
為坐標原點),求直線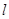 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省高三第一次月考理科數學卷 題型:解答題
(本小題滿分14分)
已知曲線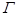 上任意一點
上任意一點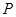 到兩個定點
到兩個定點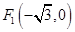 和
和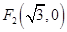 的距離之和為4.
的距離之和為4.
(1)求曲線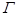 的方程;
的方程;
(2)設過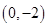 的直線
的直線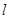 與曲線
與曲線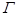 交于
交于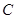 、
、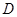 兩點,且
兩點,且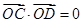 (
(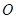 為坐標原點),求直線
為坐標原點),求直線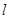 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省高三第一次月考理科數學卷 題型:解答題
(本小題滿分14分)
已知曲線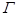 上任意一點
上任意一點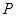 到兩個定點
到兩個定點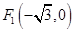 和
和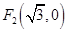 的距離之和為4.
的距離之和為4.
(1)求曲線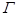 的方程;
的方程;
(2)設過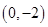 的直線
的直線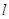 與曲線
與曲線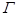 交于
交于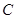 、
、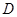 兩點,且
兩點,且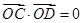 (
(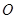 為坐標原點),求直線
為坐標原點),求直線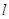 的方程.
的方程.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com