
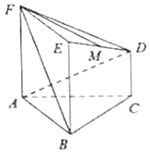
【題目】在如圖所示的幾何體中,正方形![]() 所在的平面與正三角形ABC所在的平面互相垂直,
所在的平面與正三角形ABC所在的平面互相垂直, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中點.
的中點.
(1)求證: ![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析;(2) ![]() .
.
【解析】試題分析:證明線面平則只需在平面內找一線與之平行即可,通常找中位線和建立平行四邊形來證明,本題中可以容易發現連接AE交BF于點N,連接MN,可證MN為中位線;(2)二面角的問題通常借助于空間坐標系來求解,本題中可建立如圖的坐標系,然后求出各面的法向量,再根據向量的夾角公式即可得出結論
解析:(1)連接AE交BF于點N,連接MN.
因為ABEF是正方形,所以N是AE的中點,
又M是ED的中點,所以MN∥AD.
因為AD平面BFM,MN![]() 平面BFM,
平面BFM,
所以AD∥平面BFM.
(2)因為ABEF是正方形,所以BE⊥AB,
因為平面ABEF⊥平面ABC,平面ABEF∩平面ABC=AB,
所以BE⊥平面ABC,因為CD∥BE,所以取BC的中點O,
連接OM,則OM⊥平面ABC,因為△ABC是正三角形,所以OA⊥BC,
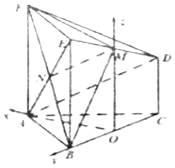
所以以O為坐標原點建立如圖所示的空間直角坐標系:
設CD=1,則B(0,1,0),E(0,1,2),D(0,﹣1,1),
![]() ,
,![]() .
.
設平面BMF的一個法向量為![]() ,
,
則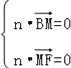 ,所以
,所以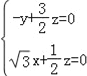 ,
,
令![]() ,則z=﹣6,y=﹣9,所以
,則z=﹣6,y=﹣9,所以![]() .
.
又因為![]() 是平面BME的法向量,
是平面BME的法向量,
所以![]() .
.
所以二面角E﹣BM﹣F的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2+10x+10y+34=0.
(Ⅰ)試寫出圓C的圓心坐標和半徑;
(Ⅱ)圓D的圓心在直線x=-5上,且與圓C相外切,被x軸截得的弦長為10,求圓D的方程;
(Ⅲ)過點P(0,2)的直線交(Ⅱ)中圓D于E,F兩點,求弦EF的中點M的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的定義域為
的定義域為![]() ,若對于任意的
,若對于任意的![]() ,,當
,,當![]() 時,都有
時,都有![]() ,則稱函數
,則稱函數![]() 在
在![]() 上為非減函數.設函數
上為非減函數.設函數![]() 在
在![]() 上為非減函數,且滿足以下三個條件:①
上為非減函數,且滿足以下三個條件:①![]() ;②
;②![]() ;③
;③![]() ,則
,則![]() 等于( ).
等于( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了解該校教師對教工食堂的滿意度情況,隨機訪問了![]() 名教師.根據這
名教師.根據這![]() 名教師對該食堂的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為:
名教師對該食堂的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為: ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() .
.
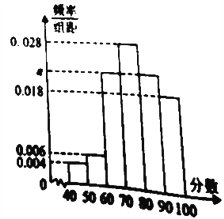
(1)求頻率分布直方圖中![]() 的值;
的值;
(2)從評分在![]() 的受訪教師中,隨機抽取2人,求此2人的評分都在
的受訪教師中,隨機抽取2人,求此2人的評分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了解該校教師對教工食堂的滿意度情況,隨機訪問了![]() 名教師.根據這
名教師.根據這![]() 名教師對該食堂的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為:
名教師對該食堂的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為: ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() .
.
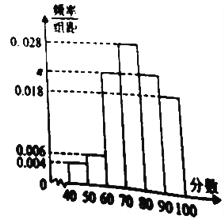
(1)求頻率分布直方圖中![]() 的值;
的值;
(2)從評分在![]() 的受訪教師中,隨機抽取2人,求此2人的評分都在
的受訪教師中,隨機抽取2人,求此2人的評分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1的參數方程是 ![]() (φ為參數),以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系,曲線C2的極坐標系方程是
(φ為參數),以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系,曲線C2的極坐標系方程是 ![]() ,正方形ABCD的頂點都在C1上,且A,B,C,D依逆時針次序排列,點A的極坐標為
,正方形ABCD的頂點都在C1上,且A,B,C,D依逆時針次序排列,點A的極坐標為 ![]() .
.
(1)求點A,B,C,D的直角坐標;
(2)設P為C2上任意一點,求|PA|2+|PB|2+|PC|2+|PD|2的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的通項公式an=5﹣n,其前n項和為Sn , 將數列{an}的前4項抽去其中一項后,剩下三項按原來順序恰為等比數列{bn}的前3項,記{bn}的前n項和為Tn , 若存在m∈N* , 使對任意n∈N* , 總有Sn<Tn+λ恒成立,則實數λ的取值范圍是( )
A.λ≥2
B.λ>3
C.λ≥3
D.λ>2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com