【題目】函數
的定義域為
，若對于任意的
，，當
時，都有
，則稱函數在上為非減函數．設函數在
上為非減函數，且滿足以下三個條件：①
；②
；③
，則
等于（ ）．
A. 
B. 
C. 
D. 
【答案】B
【解析】
由賦值法得到f（
）=
，f（
）=，再根據題中的表達式遞推得到f（
）=
，由f（）=及②
得到f（
）=，再由題中所給的非減函數得到
可得 f（）≤f（
）≤f（），進而得到結果.
令x=1，由條件求得f（1）=1，f（）=f（1）=，再由 f（）+f（）=1，由此求得f（）=.
又∵②，令x=1，可得 f（）=f（1）=．
再由③可得f（）+f（）=1，故有f（）=．
對于②，令x=1可得 f（）=f（1）=；
由此可得 f（
）=f（）=
、f（
）=f（）=
、f（
）=f（）=
、f（）= f（）=．
令x=，由f（）=及②，可得 f（
）=，f（
）=，f（
）=，f（）=．
再由可得 f（）≤f（）≤f（），即 ≤f（）≤，故 f（）=.
故答案為：B.
科目：高中數學 來源： 題型：
【題目】我國古代秦九韶算法可計算多項式anxn+an﹣1xn﹣1+…+a1x+a0的值，它所反映的程序框圖如圖所示，當x=1時，當多項式為x4+4x3+6x2+4x+1的值為（ ） 
A.5
B.16
C.15
D.11
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（1）判斷并證明函數
的奇偶性；
（2）判斷當
時函數
的單調性，并用定義證明；
（3）若
定義域為
，解不等式
.
【答案】（1）奇函數（2）增函數（3）
【解析】試題分析：（1）判斷與證明函數的奇偶性，首先要確定函數的定義域是否關于原點對稱，再判斷f(-x)與f(x)的關系，如果對定義域上的任意x，都滿足f(-x)=f(x)就是偶函數，如果f(-x)=-f(x)就是奇函數，否則是非奇非偶函數。（2）利函數單調性定義證明單調性，按假設，作差，化簡，判斷，下結論五個步驟。（3）由（1）（2）奇函數
在（-1，1）為單調函數，
原不等式變形為f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函數的單調性及定義（-1，1）求解得x范圍。
試題解析：（1）函數
為奇函數．證明如下：
定義域為
又
為奇函數
（2）函數
在（-1，1）為單調函數．證明如下：
任取
，則
， 
即
故
在（-1，1）上為增函數
（3）由（1）、（2）可得
則
解得： 
所以，原不等式的解集為
【點睛】
（1）奇偶性：判斷與證明函數的奇偶性，首先要確定函數的定義域是否關于原點對稱，再判斷f(-x)與f(x)的關系，如果對定義域上的任意x，都滿足f(-x)=f(x)就是偶函數，如果f(-x)=-f(x)就是奇函數，否則是非奇非偶函數。
（2）單調性：利函數單調性定義證明單調性，按假設，作差，化簡，定號，下結論五個步驟。
【題型】解答題
【結束】
22
【題目】已知函數
.
（1）若
的定義域和值域均是
，求實數
的值；
（2）若在區間
上是減函數，且對任意的
，都有
，求實數的取值范圍；
（3）若
，且對任意的
，都存在
，使得
成立，求實數的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】橢圓
的左、右焦點分別是
，且點
在
上，拋物線
與橢圓
交于四點
（I）求
的方程；
（Ⅱ）試探究坐標平面上是否存在定點
，滿足
?（若存在，求出
的坐標；若不存在，需說明理由.）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知P是橢圓
上的一點，F1,F2是橢圓的兩個焦點。
（1）當∠F1PF2=60°時，求△F1PF2的面積；
（2）當∠F1PF2為鈍角時，求點P橫坐標的取值范圍。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列關系式中正確的是（ ）
A. sin11°＜cos10°＜sin168° B. sin168°＜sin11°＜cos10°
C. sin11°＜sin168°＜cos10° D. sin168°＜cos10°＜sin11°
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在如圖所示的幾何體中，正方形
所在的平面與正三角形ABC所在的平面互相垂直， 
，且
， 
是
的中點．
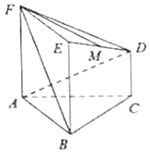
（1）求證： 
∥平面
；
（2）求二面角
的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線的標準方程是
，
（1）求它的焦點坐標和準線方程．
（2）直線L過已知拋物線的焦點且傾斜角為
，并與拋物線相交于A、B兩點，求弦AB的長度．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
