
【題目】某市縣鄉教師流失現象非常嚴重,為了縣鄉孩子們能接受良好教育,某市今年要為兩所縣鄉中學招聘儲備未來三年的教師,現在每招聘一名教師需要1萬元,若三年后教師嚴重短缺時再招聘,由于各種因素,則每招聘一名教師需要3萬元,已知現在該市縣鄉中學無多余教師,為決策應招聘多少縣鄉教師搜集并整理了該市50所縣鄉中學在過去三年內的教師流失數,得到如表的頻率分布表:
流失教師數 | 6 | 7 | 8 | 9 |
頻數 | 10 | 15 | 15 | 10 |
以這50所縣鄉中學流失教師數的頻率代替一所縣鄉中學流失教師數發生的概率,記![]() 表示兩所縣鄉中學在過去三年共流失的教師數,
表示兩所縣鄉中學在過去三年共流失的教師數, ![]() 表示今年為兩所縣鄉中學招聘的教師數.為保障縣鄉孩子教育不受影響,若未來三年內教師有短缺,則第四年馬上招聘.
表示今年為兩所縣鄉中學招聘的教師數.為保障縣鄉孩子教育不受影響,若未來三年內教師有短缺,則第四年馬上招聘.
(1)求![]() 的分布列;
的分布列;
(2)若要求![]() ,確定
,確定![]() 的最小值;
的最小值;
(3)以未來四年內招聘教師所需費用的期望值為決策依據,在![]() 與
與![]() 之中選其一,應選用哪個?
之中選其一,應選用哪個?
【答案】(1)見解析(2)15(3)![]()
【解析】【試題分析】(1)先由頻率及計算出概率,兩所學校流失教師數![]() 可能取值為
可能取值為![]() ,利用相互獨立事件的概率計算公式計算出分布列.(2)由(1)易求得
,利用相互獨立事件的概率計算公式計算出分布列.(2)由(1)易求得![]() 的最小值為15.(3)分別計算出
的最小值為15.(3)分別計算出![]() 時,招聘教師所需費用的期望值,通過對比期望值確定選
時,招聘教師所需費用的期望值,通過對比期望值確定選![]() 較為合適.
較為合適.
【試題解析】
解:(1)由頻數分布表中教師流失頻率代替教師流失概率可得,一所縣鄉中學在三年內流失的教師數為6,7,8,9的概率分別為0.2,0.3,0.3,0.2.
![]() 所有可能的取值為:12,13,14,15,16,17,18,
所有可能的取值為:12,13,14,15,16,17,18,
且![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以![]() 的分布列為:
的分布列為:
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 0.04 | 0.12 | 0.21 | 0.26 | 0.21 | 0.12 | 0.04 |
(2)由(1)知![]() ,
, ![]() ,
,
故![]() 的最小值為15.
的最小值為15.
(3)記![]() 表示兩所縣鄉中學未來四年內在招聘教師上所需的費用(單位:萬元).
表示兩所縣鄉中學未來四年內在招聘教師上所需的費用(單位:萬元).
當![]() 時,
時, ![]() 的分布列為:
的分布列為:
| 15 | 18 | 21 | 24 |
| 0.63 | 0.21 | 0.12 | 0.04 |
![]() ;
;
當![]() 時,
時, ![]() 的分布列為:
的分布列為:
| 16 | 19 | 22 |
| 0.84 | 0.12 | 0.04 |
![]() .
.
可知當![]() 時所需費用的期望值小于
時所需費用的期望值小于![]() 時所需費用的期望值,故應選
時所需費用的期望值,故應選![]() .
.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,建立極坐標系,已知直線
軸的正半軸為極軸,建立極坐標系,已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,點
兩點,點![]() 為
為![]() 的中點,點
的中點,點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學每年暑假舉行“學科思維講座”活動,每場講座結束時,所有聽講這都要填寫一份問卷調查.2017年暑假某一天五場講座收到的問卷份數情況如下表:
學科 | 語文 | 數學 | 英語 | 理綜 | 文綜 |
問卷份數 |
|
|
|
|
|
用分層抽樣的方法從這一天的所有問卷中抽取![]() 份進行統計,結果如下表:
份進行統計,結果如下表:
滿意 | 一般 | 不滿意 | |
語文 |
|
|
|
數學 |
| 1 |
|
英語 |
|
|
|
理綜 |
|
|
|
文綜 |
|
|
|
(1)估計這次講座活動的總體滿意率;
(2)求聽數學講座的甲某的調查問卷被選中的概率;
(3)若想從調查問卷被選中且填寫不滿意的人中再隨機選出![]() 人進行家訪,求這
人進行家訪,求這![]() 人中選擇的是理綜講座的人數的分布列.
人中選擇的是理綜講座的人數的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直三棱柱![]() 中,底面為等腰直角三角形,
中,底面為等腰直角三角形, ![]() ,
, ![]() , 若
, 若![]() 、
、![]() 、
、![]() 別是棱
別是棱![]() 、
、![]() 、
、![]() 的中點,則下列四個命題:
的中點,則下列四個命題:
![]() ;
;
②三棱錐![]() 的外接球的表面積為
的外接球的表面積為![]() ;
;
③三棱錐![]() 的體積為
的體積為![]() ;
;
④直線![]() 與平面
與平面![]() 所成角為
所成角為![]()
其中正確的命題有__________.(把所有正確命題的序號填在答題卡上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為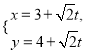 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,并使得它與直角坐標系
軸的正半軸為極軸建立極坐標系,并使得它與直角坐標系![]() 有相同的長度單位,曲線
有相同的長度單位,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 與直線
與直線![]() 交于
交于![]() 、
、![]() 兩點,且
兩點,且![]() 點的坐標為
點的坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 的底面
的底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,點
,點![]() 在線段
在線段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)當四棱錐![]() 的體積最大時,求平面
的體積最大時,求平面![]() 與平面
與平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() 的對稱軸與準線的交點,點
的對稱軸與準線的交點,點![]() 為拋物線的焦點,
為拋物線的焦點, ![]() 在拋物線上且滿足
在拋物線上且滿足![]() ,當
,當![]() 取最大值時,點
取最大值時,點![]() 恰好在以
恰好在以![]() ,
, ![]() 為焦點的雙曲線上,則雙曲線的離心率為( )
為焦點的雙曲線上,則雙曲線的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知梯形![]() 如圖(1)所示,其中
如圖(1)所示,其中![]() ,
, ![]() ,四邊形
,四邊形![]() 是邊長為
是邊長為![]() 的正方形,現沿
的正方形,現沿![]() 進行折疊,使得平面
進行折疊,使得平面![]() 平面
平面![]() ,得到如圖(2)所示的幾何體.
,得到如圖(2)所示的幾何體.

(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知點![]() 在線段
在線段![]() 上,且
上,且![]() 平面
平面![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點重合,且過點
的焦點重合,且過點![]() .過點
.過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,
兩點, ![]() 為橢圓的左頂點.
為橢圓的左頂點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)求![]() 面積的最大值,并求此時直線
面積的最大值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com