
【題目】已知![]() 是數列
是數列![]() 的前
的前![]() 項和,
項和,![]() 且
且![]() ,
,![]() ,數列
,數列![]() 中,
中,![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設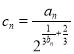 ,求
,求![]() 的前
的前![]() 項和
項和![]() ;
;
(3)證明:對一切![]() ,
,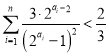
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)見解析
;(3)見解析
【解析】
(1)當![]() 時,構造
時,構造![]() ,變形為
,變形為![]() ,再求數列的通項公式;
,再求數列的通項公式;
(2)由已知變形為![]() ,利用累加法求數列
,利用累加法求數列![]() 的通項公式,然后再求數列
的通項公式,然后再求數列![]() 的通項公式,利用錯位相減法求和;
的通項公式,利用錯位相減法求和;
(3)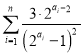 表示求數列
表示求數列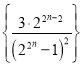 的前
的前![]() 項和,然后將通項放縮為
項和,然后將通項放縮為![]() 時,
時,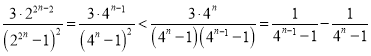 ,然后利用裂項相消法求和.
,然后利用裂項相消法求和.
(1)![]() 時,可得
時,可得![]() ,
,
![]() 時,
時,![]() ,
,![]() ,兩式相減,
,兩式相減,
得![]() ,
,![]() ,
,
![]() ,
,
![]() 數列
數列![]() 的奇數項和偶數項分別成以4為公差的等差數列,
的奇數項和偶數項分別成以4為公差的等差數列,
當![]() ,
,![]() 時,
時,![]() ,
,
當![]() ,
,![]() 時,
時,![]() ,
,
![]() ,
,![]() .
.
(2)![]()
![]() ,
,
![]() ,即
,即![]() ,
,
整理為:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…………………………,
![]() ,
,![]() 時,
時,
這![]() 個式子相加可得
個式子相加可得![]() ,
,
![]() ,當
,當![]() 時,
時,![]() 成立,
成立,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
兩式相減可得:![]()
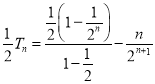 ,
,
![]()
(3)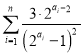 表示求數列
表示求數列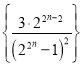 的前
的前![]() 項和,設前
項和,設前![]() 項和為
項和為![]() ,
,
當![]() 時,
時,![]() 成立,
成立,
當![]() 時,
時,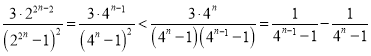
![]()
![]() .
.
綜上可知![]() ,
,
![]() 對一切
對一切![]() ,
,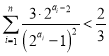 .
.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數學 來源: 題型:
【題目】[選修4―4:坐標系與參數方程]
在直角坐標系xOy中,曲線C的參數方程為![]() (θ為參數),直線l的參數方程為
(θ為參數),直線l的參數方程為![]() .
.
(1)若a=1,求C與l的交點坐標;
(2)若C上的點到l的距離的最大值為![]() ,求a.
,求a.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]() .
.

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年森林城市建設座談會在深圳舉行.會上宣讀了國家森林城市稱號批準決定,并舉行授牌儀式,滕州市榜上有名,被正式批準為“國家森林城市”.為進一步推進國家森林城市建設,我市準備制定生態環境改造投資方案,該方案要求同時具備下列兩個條件:
①每年用于風景區改造的費用![]() 隨每年改造生態環境總費用
隨每年改造生態環境總費用![]() 增加而增加;②每年用于風景區改造的費用
增加而增加;②每年用于風景區改造的費用![]() 不得低于每年改造生態環境總費用
不得低于每年改造生態環境總費用![]() 的15%,但不得高于每年改造生態環境總費用
的15%,但不得高于每年改造生態環境總費用![]() 的25%.若每年改造生態環境的總費用至少1億元,至多4億元;請你分析能否采用函數模型
的25%.若每年改造生態環境的總費用至少1億元,至多4億元;請你分析能否采用函數模型![]() 作為生態環境改造投資方案.
作為生態環境改造投資方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,![]() 是邊長為2的正三角形,
是邊長為2的正三角形,![]() 平面ABC,平面
平面ABC,平面![]() 平面ABC,
平面ABC,![]() ,且
,且![]() .
.
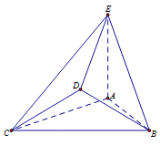
(1)若![]() ,求證:
,求證:![]() 平面BDE;
平面BDE;
(2)若二面角![]() 為
為![]() ,求直線CD與平面BDE所成角.
,求直線CD與平面BDE所成角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且點
,且點![]() 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)若橢圓![]() 的焦點在
的焦點在![]() 軸上,點
軸上,點![]() 為坐標原點,射線
為坐標原點,射線![]() 、
、![]() 分別與橢圓
分別與橢圓![]() 交于點
交于點![]() 、點
、點![]() ,且
,且![]() ,試判斷直線
,試判斷直線![]() 與圓
與圓![]() :
:![]() 的位置關系,并證明你的結論.
的位置關系,并證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com