
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]() .
.

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)根據題設條件可以得出AB⊥AP,CD⊥PD.而AB//CD,就可證明出AB⊥平面PAD.
進而證明出平面PAB⊥平面PAD.(2)先找出AD中點,找出相互垂直的線,建立以![]() 為坐標原點,
為坐標原點, ![]() 的方向為
的方向為![]() 軸正方向,
軸正方向, ![]() 為單位長的空間直角坐標系,列出所需要的點的坐標,設
為單位長的空間直角坐標系,列出所需要的點的坐標,設![]() 是平面
是平面![]() 的法向量,
的法向量, ![]() 是平面
是平面![]() 的法向量,根據垂直關系,求出
的法向量,根據垂直關系,求出![]() 和
和![]() ,利用數量積公式可求出二面角的平面角.
,利用數量積公式可求出二面角的平面角.
試題解析:(1)由已知![]() ,得AB⊥AP,CD⊥PD.
,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,從而AB⊥平面PAD.
又AB ![]() 平面PAB,所以平面PAB⊥平面PAD.
平面PAB,所以平面PAB⊥平面PAD.
(2)在平面![]() 內做
內做![]() ,垂足為
,垂足為![]() ,
,
由(1)可知, ![]() 平面
平面![]() ,故
,故![]() ,可得
,可得![]() 平面
平面![]() .
.
以![]() 為坐標原點,
為坐標原點, ![]() 的方向為
的方向為![]() 軸正方向,
軸正方向, ![]() 為單位長,建立如圖所示的空間直角坐標系
為單位長,建立如圖所示的空間直角坐標系![]() .
.

由(1)及已知可得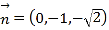 ,
,  ,
, 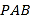 ,
, 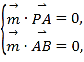 .
.
所以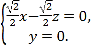 ,
, ![]() ,
,  ,
, ![]() .
.
設![]() 是平面
是平面![]() 的法向量,則
的法向量,則
![]() ,即
,即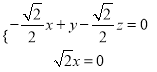 ,
,
可取![]() .
.
設![]() 是平面
是平面![]() 的法向量,則
的法向量,則
![]() ,即
,即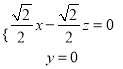 ,
,
可取![]() .
.
則 ,
,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.
點睛:高考對空間向量與立體幾何的考查主要體現在以下幾個方面:①求異面直線所成的角,關鍵是轉化為兩直線的方向向量的夾角;②求直線與平面所成的角,關鍵是轉化為直線的方向向量和平面的法向量的夾角;③求二面角,關鍵是轉化為兩平面的法向量的夾角.建立空間直角坐標系和表示出所需點的坐標是解題的關鍵.


科目:高中數學 來源: 題型:
【題目】旅行社為某旅行團包飛機去旅游,其中旅行社的包機費為![]() 元.旅行團中的每個人的飛機票按以下方式與旅行社結算:若旅行團的人數不超過
元.旅行團中的每個人的飛機票按以下方式與旅行社結算:若旅行團的人數不超過![]() 人時,飛機票每張收費
人時,飛機票每張收費![]() 元;若旅行團的人數多于
元;若旅行團的人數多于![]() 人時,則予以優惠,每多
人時,則予以優惠,每多![]() 人,每個人的機票費減少
人,每個人的機票費減少![]() 元,但旅行團的人數最多不超過
元,但旅行團的人數最多不超過![]() 人.設旅行團的人數為
人.設旅行團的人數為![]() 人,飛機票價格
人,飛機票價格![]() 元,旅行社的利潤為
元,旅行社的利潤為![]() 元.
元.
(1)寫出飛機票價格![]() 元與旅行團人數
元與旅行團人數![]() 之間的函數關系式;
之間的函數關系式;
(2)當旅行團人數![]() 為多少時,旅行社可獲得最大利潤?求出最大利潤.
為多少時,旅行社可獲得最大利潤?求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的漸近線方程為
的漸近線方程為![]() ,左焦點為F,過
,左焦點為F,過![]() 的直線為
的直線為![]() ,原點到直線
,原點到直線![]() 的距離是
的距離是![]()
(1)求雙曲線的方程;
(2)已知直線![]() 交雙曲線于不同的兩點C,D,問是否存在實數
交雙曲線于不同的兩點C,D,問是否存在實數![]() ,使得以CD為直徑的圓經過雙曲線的左焦點F。若存在,求出m的值;若不存在,請說明理由。
,使得以CD為直徑的圓經過雙曲線的左焦點F。若存在,求出m的值;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】朱載堉(1536~1611),是中國明代一位杰出的音樂家、數學家和天文歷算家,他的著作《律學新說》中制成了最早的“十二平均律”.十二平均律是目前世界上通用的把一組音(八度)分成十二個半音音程的律制,各相鄰兩律之間的頻率之比完全相等,亦稱“十二等程律”.即一個八度13個音,相鄰兩個音之間的頻率之比相等,且最后一個音是最初那個音的頻率的2倍.設第三個音的頻率為![]() ,第七個音的頻率為
,第七個音的頻率為![]() ,則
,則![]() =
=
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列{an}中,a1=![]() ,其前n項和為Sn,且Sn=an+1-
,其前n項和為Sn,且Sn=an+1-![]() (n∈N*).
(n∈N*).
(1)求an,Sn;
(2)設bn=log2(2Sn+1)-2,數列{cn}滿足cn·bn+3·bn+4=1+(n+1)(n+2)·2bn,數列{cn}的前n項和為Tn,求使4Tn>2n+1-![]() 成立的最小正整數n的值.
成立的最小正整數n的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com