
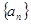 的各項均為正數,Sn為其前n項和,對于任意
的各項均為正數,Sn為其前n項和,對于任意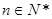 ,滿足關系
,滿足關系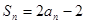 .
. 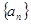 是等比數列;
是等比數列;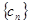 中,設
中,設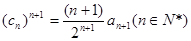 ,求數列
,求數列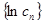 中的最大項.
中的最大項. 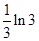
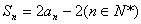 ①
①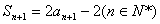 ②
② 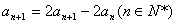
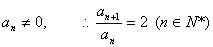 故數列
故數列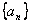 是等比數列
是等比數列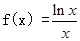 ,∵在區間(0,e)上,f'(x)>0,在區間(e,+∞)上,f'(x)<0.在區間(e,+∞)上f(x)為單調遞減函數.(12分)
,∵在區間(0,e)上,f'(x)>0,在區間(e,+∞)上,f'(x)<0.在區間(e,+∞)上f(x)為單調遞減函數.(12分)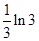


科目:高中數學 來源:不詳 題型:單選題
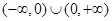 上的函數
上的函數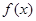 ,如果對于任意給定的等比數列
,如果對于任意給定的等比數列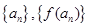 仍是等比數列,則稱
仍是等比數列,則稱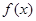 為“保等比數列函數”。現有定義在
為“保等比數列函數”。現有定義在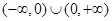 上的如下函數:①
上的如下函數:①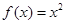 ;②
;②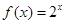 ;③
;③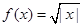 ;④
;④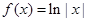 。則其中是“保等比數列函數”的
。則其中是“保等比數列函數”的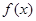 的序號為
的序號為| A.①② | B.③④ | C.①③ | D.②④ |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
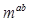 <1,則m的取值范圍是( )
<1,則m的取值范圍是( )| A.m>1 | B.1<m<8 |
| C.m>8 | D.0<m<1或m>8 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
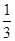 為第三項,9為第六項的等比數列的公比,則這個三角形是
為第三項,9為第六項的等比數列的公比,則這個三角形是| A.鈍角三角形 | B.銳角三角形 | C.等腰直角三角形 | D.以上都不對 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com