
【題目】已知數列{an}滿足:a1+a2+a3+…+an=n-an,(n=1,2,3,…)
(Ⅰ)求證:數列{an-1}是等比數列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果對任意n∈N*,都有bn+![]() t≤t2,求實數t的取值范圍.
t≤t2,求實數t的取值范圍.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩名大學生因為學習需要,欲各自選購一臺筆記本電腦,他們決定在A,B,C三個品牌的五款產品中選擇,這五款筆記本電腦在某電商平臺的價格與銷量數據如表所示:
品牌 | A | B | C | ||
型號 | A﹣1 | A﹣2 | B﹣1 | B﹣2 | C﹣1 |
價格(元) | 6000 | 7500 | 10000 | 8000 | 4500 |
銷量(臺) | 1000 | 1000 | 200 | 800 | 3000 |
(Ⅰ)若甲選擇某品牌的筆記本電腦的概率與該品牌的總銷量成正比,求他選擇B品牌的筆記本電腦的概率;
(Ⅱ)若甲、乙兩人選擇每種型號的筆記本電腦的概率都相等,且兩人選購的型號不相同,求他們兩人購買的筆記本電腦的價格之和大于15000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高二理科8班共有50名學生參加學業水平模擬考試,成績(單位:分,滿分100分)大于或等于90分的為優秀,其中語文成績近似服從正態分布![]() ,數學成績的頻率分布直方圖如圖.
,數學成績的頻率分布直方圖如圖.
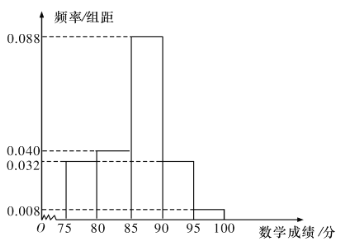
(I)這50名學生中本次考試語文、數學成績優秀的大約各有多少人?
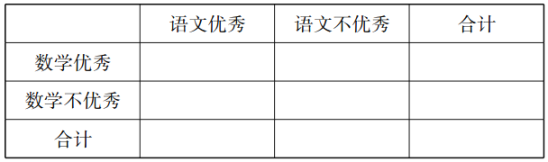
(Ⅱ)如果語文和數學兩科成績都優秀的共有4人,從語文優秀或數學優秀的這些同學中隨機抽取3人,設3人中兩科都優秀的有![]() 人,求
人,求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅲ)根據(I)(Ⅱ)的數據,是否有99%以上的把握認為語文成績優秀的同學,數學成績也優秀?
附:①若![]() ~
~![]() ,則
,則![]() ,
,![]() ;
;
②![]() ;
;
③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() 交于點
交于點![]() ,
,![]() 是
是![]() 上任意一點.
上任意一點.
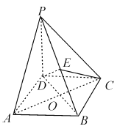
(1)求證![]() ;
;
(2)已知二面角![]() 的余弦值為
的余弦值為![]() ,若
,若![]() 為
為![]() 的中點,求
的中點,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 與
與![]() 軸交于
軸交于![]() 兩點,且
兩點,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 是橢圓
是橢圓![]() 上的一個動點,且直線
上的一個動點,且直線![]() 與直線
與直線![]() 分別交于
分別交于![]() 兩點.是否存在點
兩點.是否存在點![]() 使得以
使得以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ?若存在,求出點
?若存在,求出點![]() 的橫坐標;若不存在,說明理由.
的橫坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以該直角坐標系的原點
為參數),以該直角坐標系的原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)分別求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,交曲線
兩點,交曲線![]() 于
于![]() ,
,![]() 兩點,求
兩點,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解高一學生的心理健康狀況,某校心理健康咨詢中心對該校高一學生的睡眠狀況進行了抽樣調查.該中心隨機抽取了60名高一男生和40名高一女生,統計了他們入學第一個月的平均每天睡眠時間,得到如下頻數分布表.規定:“平均每天睡眠時間大于等于8小時”為“睡眠充足”,“平均每天睡眠時間小于8小時”為“睡眠不足”.
高一男生平均每天睡眠時間頻數分布表
睡眠時間(小時) |
|
|
|
|
|
頻數 | 3 | 20 | 19 | 10 | 8 |
高一女生平均每天睡眠時間頻數分布表
睡眠時間(小時) |
|
|
|
|
|
頻數 | 20 | 11 | 5 | 2 |
(1)請將下面的列聯表補充完整,并根據已完成的![]() 列聯表,判斷是否有
列聯表,判斷是否有![]() 的把握認為“睡眠是否充足與性別有關”?
的把握認為“睡眠是否充足與性別有關”?
睡眠充足 | 睡眠不足 | 合計 | |
男生 | 42 | ||
女生 | 7 | ||
合計 | 100 |
(2)由樣本估計總體的思想,根據這兩個頻數分布表估計該校全體高一學生入學第一個月的平均每天睡眠時間(同一組中的數據以這組數據所在區間中點的值作代表);
(3)若再從這100人中平均每天睡眠時間不足6小時的同學里隨機抽取兩人進行心理健康干預,則抽取的兩人中包含女生的概率是多少?
附:參考公式:![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com