【題目】設
、
、
是三條不同的直線，
、
、
是三個不同的平面，給出下列四個命題：
①若
，
，
，
，
，則
；
②若
，
，則
；
③若，是兩條異面直線，
，
，
，
且，則
；
④若
，，
，，，則
.
其中正確命題的序號是（ ）
A.①③B.①④C.②③D.②④
【答案】A
【解析】
根據線面平行的性質定理以及空間中平行直線的傳遞性可判斷出命題①的正誤；根據面面關系可判斷出命題②的正誤；利用線面平行的性質定理以及直線與平面垂直的判定定理可判斷出命題③的正誤；根據線面垂直的判定定理、面面垂直的判定定理可判斷出命題④的正誤.
對于命題①，
，
，
，由直線與平面平行的性質定理可得
，
，
，由平行線的傳遞性可知
，命題①正確；
對于命題②，
，
，則平面
與平面
平行或相交，命題②錯誤；
對于命題③，過直線
作平面
，使得
，
，
，
，
，，
，若
，根據平行線的傳遞性可得
，這與題意矛盾，
又
、
，
，
，
，又
，
、，
，
命題③正確；
對于命題④，，
，
，
，但、
不一定垂直，則
與不一定垂直，所以與也不一定垂直，命題④錯誤.
因此，正確的命題序號為①③.
故選：A.
藍天教育暑假優化學習系列答案科目：高中數學 來源： 題型：
【題目】如圖：已知某公園的四處景觀分別位于等腰梯形
的四個頂點處，其中
，
兩地的距離為
千米，
，
兩地的距離為
千米，
.現擬規劃在
(不包括端點)路段上增加一個景觀
，并建造觀光路直接通往處，造價為每千米
萬元，又重新裝飾
路段，造價為每千米
萬元.
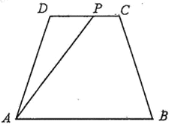
(1)若擬修建觀光路
路段長為
千米，求路段的造價；
(2)設
，當
為何值時，，段的總造價最低.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
： 
經過橢圓
： 
的左右焦點
，且與橢圓
在第一象限的交點為
，且
三點共線，直線
交橢圓
于
， 
兩點，且
（
）.
（1）求橢圓
的方程；
（2）當三角形
的面積取得最大值時，求直線
的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某數學小組到進行社會實踐調查，了解鑫鑫桶裝水經營部在為如何定價發愁。進一步調研了解到如下信息：該經營部每天的房租、人員工資等固定成本為200元，每桶水的進價是5元，銷售單價與日均銷售量的關系如下表：
銷售單價/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
日均銷售量/桶 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
根據以上信息，你認為該經營部定價為多少才能獲得最大利潤？（ ）
A.每桶8.5元B.每桶9.5元C.每桶10.5元D.每桶11.5元
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】《中華人民共和國道路交通安全法》第47條的相關規定：機動車行經人行橫道時，應當減速慢行；遇行人正在通過人行橫道，應當停車讓行，俗稱“禮讓斑馬線”，《中華人民共和國道路交通安全法》第90條規定：對不禮讓行人的駕駛員處以扣3分，罰款50元的處罰．
（1）交警從這5個月內通過該路口的駕駛員中隨機抽查了50人，調查駕駛員不“禮讓斑馬線”行為與駕齡的關系，得到如下列聯表：能否據此判斷有97.5%的把握認為“禮讓斑馬線”行為與駕齡有關？
不禮讓斑馬線 | 禮讓斑馬線 | 合計 | |
駕齡不超過1年 | 22 | 8 | 30 |
駕齡1年以上 | 8 | 12 | 20 |
合計 | 30 | 20 | 50 |
（2）下圖是某市一主干路口監控設備所抓拍的5個月內駕駛員不“禮讓斑馬線”行為的折線圖：
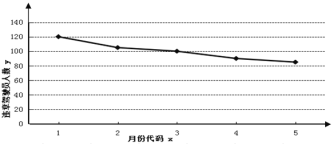
請結合圖形和所給數據求違章駕駛員人數y與月份x之間的回歸直線方程
，并預測該路口7月份的不“禮讓斑馬線”違章駕駛員人數．
附注：參考數據：
，
．
參考公式：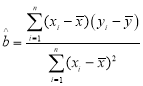
，
，
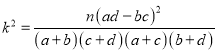（其中
）
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
