
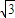 ),即可得到直線AB,直線AC及直線BC的方程,設三角形內任一點P(m,n),利用點到直線的距離公式求出P到三邊的距離之和得到為定值即可.
),即可得到直線AB,直線AC及直線BC的方程,設三角形內任一點P(m,n),利用點到直線的距離公式求出P到三邊的距離之和得到為定值即可. 解:先設等邊三角形的邊長為2a,以BC所在的直線為x軸,
解:先設等邊三角形的邊長為2a,以BC所在的直線為x軸,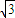 )設三角形內任一點P(m,n),
)設三角形內任一點P(m,n),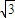 ,
,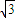 (x+a),化簡得
(x+a),化簡得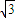 x-y+
x-y+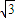 a=0;
a=0;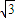 ,
,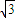 (x-a),
(x-a),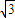 x+y-
x+y-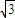 a=0;
a=0;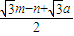 |+|
|+|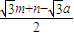 |+|n|=
|+|n|=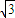 a,
a,

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com