
【題目】已知函數![]()
(1)討論![]() 的單調性;
的單調性;
(2)當![]() 時,
時,![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]()
【解析】
(1)f′(x)=(x+1)ex-ax-a=(x+1)(ex-a).對a分類討論,即可得出單調性.
(2)由xex-ax-a+1≥0,可得a(x+1)≤xex+1,當x=-1時,0≤-![]() +1恒成立.當x>-1時,a
+1恒成立.當x>-1時,a![]() 令g(x)=
令g(x)=![]() ,利用導數研究函數的單調性極值與最值即可得出.
,利用導數研究函數的單調性極值與最值即可得出.
解法一:(1)![]()
①當![]() 時,
時,
|
| -1 |
|
| - | 0 | + |
| ↘ | 極小值 | ↗ |
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 單調遞增.
單調遞增.
②當![]() 時,
時,![]() 的根為
的根為![]() 或
或![]() .
.
若![]() ,即
,即![]() ,
,
|
| -1 |
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 極大值 | ↘ | 極小值 | ↗ |
所以![]() 在
在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
若![]() ,即
,即![]() ,
,
![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上單調遞增,無減區間.
上單調遞增,無減區間.
若![]() ,即
,即![]() ,
,
|
|
|
| -1 |
|
| + | 0 | - | 0 | + |
| ↗ | 極大值 | ↘ | 極小值 | ↗ |
所以![]() 在
在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
綜上:
當![]() 時,
時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() 在
在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;
自![]() 時,
時,![]() 在
在![]() 上單調遞增,無減區間;
上單調遞增,無減區間;
當![]() 時,
時,![]() 在
在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(2)因為![]() ,所以
,所以![]() .
.
當![]() 時,
時,![]() 恒成立.
恒成立.
當![]() 時,
時,![]() .
.
令![]() ,
,![]() ,
,
設![]() ,
,
因為![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上單調遞增.
上單調遞增.
又因為![]() ,所以
,所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
則![]() ,所以
,所以![]() .
.
綜上,![]() 的取值范圍為
的取值范圍為![]() .
.
解法二:(1)同解法一;
(2)令![]() ,
,
所以![]() ,
,
當![]() 時,
時,![]() ,則
,則![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,滿足題意.
,滿足題意.
當![]() 時,
時,
令![]() ,
,
因為![]() ,即
,即![]() 在
在![]() 上單調遞增.
上單調遞增.
又因為![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有唯一的解,記為
上有唯一的解,記為![]() ,
,
|
|
|
|
| - | 0 | + |
| ↘ | 極小值 | ↗ |
![]()
![]()
![]() ,滿足題意.
,滿足題意.
當![]() 時,
時,![]() ,不滿足題意.
,不滿足題意.
綜上,![]() 的取值范圍為
的取值范圍為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩名同學參加一項射擊游戲,兩人約定,其中任何一人每射擊一次,擊中目標得2分,未擊中目標得0分.若甲、乙兩名同學射擊的命中率分別為![]() 和p,且甲、乙兩人各射擊一次所得分數之和為2的概率為
和p,且甲、乙兩人各射擊一次所得分數之和為2的概率為![]() ,假設甲、乙兩人射擊互不影響.
,假設甲、乙兩人射擊互不影響.
(1)求p的值;
(2)記甲、乙兩人各射擊一次所得分數之和為X,求X的分布列和均值![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列{an}中,a2=-8,a6=0.
(1)求數列{an}的通項公式;
(2)若等比數列{bn}滿足b1=-8,b2=a1+a2+a3,求數列{bn}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現代城市大多是棋盤式布局(如北京道路幾乎都是東西和南北走向).在這樣的城市中,我們說的兩點間的距離往往不是指兩點間的直線距離(位移),而是實際路程(如圖).在直角坐標平面內,我們定義![]() ,
,![]() 兩點間的“直角距離”為:
兩點間的“直角距離”為:![]() .
.
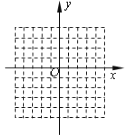
(1)在平面直角坐標系中,寫出所有滿足到原點的“直角距離”為2的“格點”的坐標.(格點指橫、縱坐標均為整數的點)
(2)求到兩定點![]() 、
、![]() 的“直角距離”和為定值
的“直角距離”和為定值![]() 的動點軌跡方程,并在直角坐標系內作出該動點的軌跡.(在以下三個條件中任選一個做答)
的動點軌跡方程,并在直角坐標系內作出該動點的軌跡.(在以下三個條件中任選一個做答)
①![]() ,
,![]() ,
,![]() ;
;
②![]() ,
,![]() ,
,![]() ;
;
③![]() ,
,![]() ,
,![]() .
.
(3)寫出同時滿足以下兩個條件的“格點”的坐標,并說明理由(格點指橫、縱坐標均為整數的點).
①到![]() ,
,![]() 兩點“直角距離”相等;
兩點“直角距離”相等;
②到![]() ,
,![]() 兩點“直角距離”和最小.
兩點“直角距離”和最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,從參加環保知識競賽的1200名學生中抽出![]() 名,將其成績(均為整數)整理后畫出的頻率分布直方圖如下:觀察圖形,回答下列問題:
名,將其成績(均為整數)整理后畫出的頻率分布直方圖如下:觀察圖形,回答下列問題:

(1)![]() 這一組的頻數、頻率分別是多少?
這一組的頻數、頻率分別是多少?
(2)估計這次環保知識競賽的及格率。(![]() 分及以上為及格)
分及以上為及格)
(3)若準備取成績最好的300名發獎,則獲獎的最低分數約為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,棱長為2,M,N分別為A1B,AC的中點.
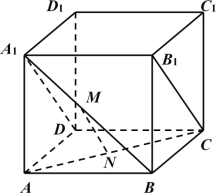
(1)證明:MN//B1C;
(2)求A1B與平面A1B1CD所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,隨著我國汽車消費水平的提高,二手車流通行業得到迅猛發展.某汽車交易市場對2017年成交的二手車交易前的使用時間(以下簡稱“使用時間”)進行統計,得到頻率分布直方圖如圖1.
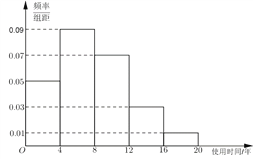

圖1 圖2
(1)記“在![]() 年成交的二手車中隨機選取一輛,該車的使用年限在
年成交的二手車中隨機選取一輛,該車的使用年限在![]() ”為事件
”為事件![]() ,試估計
,試估計![]() 的概率;
的概率;
(2)根據該汽車交易市場的歷史資料,得到散點圖如圖2,其中![]() (單位:年)表示二手車的使用時間,
(單位:年)表示二手車的使用時間,![]() (單位:萬元)表示相應的二手車的平均交易價格.由散點圖看出,可采用
(單位:萬元)表示相應的二手車的平均交易價格.由散點圖看出,可采用![]() 作為二手車平均交易價格
作為二手車平均交易價格![]() 關于其使用年限
關于其使用年限![]() 的回歸方程,相關數據如下表(表中
的回歸方程,相關數據如下表(表中![]() ,
,![]() ):
):
|
|
|
|
|
|
5.5 | 8.7 | 1.9 | 301.4 | 79.75 | 385 |
①根據回歸方程類型及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
②該汽車交易市場對使用8年以內(含8年)的二手車收取成交價格![]() 的傭金,對使用時間8年以上(不含8年)的二手車收取成交價格
的傭金,對使用時間8年以上(不含8年)的二手車收取成交價格![]() 的傭金.在圖1對使用時間的分組中,以各組的區間中點值代表該組的各個值.若以2017年的數據作為決策依據,計算該汽車交易市場對成交的每輛車收取的平均傭金.
的傭金.在圖1對使用時間的分組中,以各組的區間中點值代表該組的各個值.若以2017年的數據作為決策依據,計算該汽車交易市場對成交的每輛車收取的平均傭金.
附注:①對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ;
;
②參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某水果種植基地引進一種新水果品種,經研究發現該水果每株的產量![]() (單位:
(單位:![]() )和與它“相近”的株數
)和與它“相近”的株數![]() 具有線性相關關系(兩株作物“相近”是指它們的直線距離不超過
具有線性相關關系(兩株作物“相近”是指它們的直線距離不超過![]() ),并分別記錄了相近株數為0,1,2,3,4時每株產量的相關數據如下:
),并分別記錄了相近株數為0,1,2,3,4時每株產量的相關數據如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出該種水果每株的產量![]() 關于它“相近”株數
關于它“相近”株數![]() 的回歸方程;
的回歸方程;
(2)有一種植戶準備種植該種水果500株,且每株與它“相近”的株數都為![]() ,計劃收獲后能全部售出,價格為10元
,計劃收獲后能全部售出,價格為10元![]() ,如果收入(收入=產量×價格)不低于25000元,則
,如果收入(收入=產量×價格)不低于25000元,則![]() 的最大值是多少?
的最大值是多少?
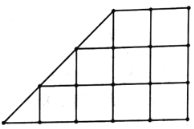
(3)該種植基地在如圖所示的直角梯形地塊的每個交叉點(直線的交點)處都種了一株該種水果,其中每個小正方形的邊長和直角三角形的直角邊長都為![]() ,已知該梯形地塊周邊無其他樹木影響,若從所種的該水果中隨機選取一株,試根據(1)中的回歸方程,預測它的產量的分布列與數學期望.
,已知該梯形地塊周邊無其他樹木影響,若從所種的該水果中隨機選取一株,試根據(1)中的回歸方程,預測它的產量的分布列與數學期望.
附:回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為: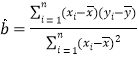 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】市面上有某品牌![]() 型和
型和![]() 型兩種節能燈,假定
型兩種節能燈,假定![]() 型節能燈使用壽命都超過5000小時,經銷商對
型節能燈使用壽命都超過5000小時,經銷商對![]() 型節能燈使用壽命進行了調查統計,得到如下頻率分布直方圖:
型節能燈使用壽命進行了調查統計,得到如下頻率分布直方圖:

某商家因原店面需要重新裝修,需租賃一家新店面進行周轉,合約期一年.新店面需安裝該品牌節能燈5支(同種型號)即可正常營業.經了解,![]() 型20瓦和
型20瓦和![]() 型55瓦的兩種節能燈照明效果相當,都適合安裝.已知
型55瓦的兩種節能燈照明效果相當,都適合安裝.已知![]() 型和
型和![]() 型節能燈每支的價格分別為120元、25元,當地商業電價為0.75元/千瓦時.假定該店面一年周轉期的照明時間為3600小時,若正常營業期間燈壞了立即購買同型燈管更換.(用頻率估計概率)
型節能燈每支的價格分別為120元、25元,當地商業電價為0.75元/千瓦時.假定該店面一年周轉期的照明時間為3600小時,若正常營業期間燈壞了立即購買同型燈管更換.(用頻率估計概率)
(Ⅰ)根據頻率直方圖估算![]() 型節能燈的平均使用壽命;
型節能燈的平均使用壽命;
(Ⅱ)根據統計知識知,若一支燈管一年內需要更換的概率為![]() ,那么
,那么![]() 支燈管估計需要更換
支燈管估計需要更換![]() 支.若該商家新店面全部安裝了
支.若該商家新店面全部安裝了![]() 型節能燈,試估計一年內需更換的支數;
型節能燈,試估計一年內需更換的支數;
(Ⅲ)若只考慮燈的成本和消耗電費,你認為該商家應選擇哪種型號的節能燈,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com